题目内容
若函数f(2x-1)为偶函数,则函数f(2x+1)的对称轴是 .
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:根据函数奇偶性的性质即可得到结论.
解答:
解:∵函数f(2x-1)为偶函数,
∴函数f(2x-1)的对称轴为x=0,
∵f(2x+1)=f(2x-1+2)=f[2(x+1)-1],
∴将f(2x-1)沿着x轴向左平移1个单位即可得到f(2x+1),
此时函数f(2x+1)的对称轴为x=-1,
故答案为:x=-1.
∴函数f(2x-1)的对称轴为x=0,
∵f(2x+1)=f(2x-1+2)=f[2(x+1)-1],
∴将f(2x-1)沿着x轴向左平移1个单位即可得到f(2x+1),
此时函数f(2x+1)的对称轴为x=-1,
故答案为:x=-1.
点评:本题主要考查函数奇偶性的对称性,利用函数平移之间的关系,利用平移关系是解决本题的关键.

练习册系列答案
相关题目
某小组有3名男生和2名女生,从中任选2名同学参加演讲比赛.下列各对事件中,为对立事件的是( )
| A、恰有一名男生和恰有2名男生 |
| B、至少一名男生和至少一名女生 |
| C、至少有一名男生和与全是女生 |
| D、至少有一名男生和全是男生 |
 某样本数据的频率分布直方图的部分图形如图所示,则数据在[50,70)的频率约为( )
某样本数据的频率分布直方图的部分图形如图所示,则数据在[50,70)的频率约为( )| A、0.25 | B、0.5 |
| C、0.05 | D、0.025 |
若复数z满足z(1+2i)=3-4i(i为虚数单位),则z的共轭复数是( )
| A、-1+2i | B、-1-2i |
| C、1+2i | D、1-2i |
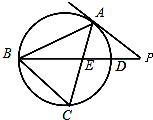 如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,PB交AC于点E,交⊙O于点D,若PE=PA,∠ABC=60°,PD=1,BD=8,则BC=
如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,PB交AC于点E,交⊙O于点D,若PE=PA,∠ABC=60°,PD=1,BD=8,则BC=