题目内容
6.已知f(x)满足对?x∈R,f(-x)+f(x)=0,且当x≤0时,f(x)=$\frac{1}{{e}^{x}}$+k(k为常数),则f(ln5)的值为( )| A. | 4 | B. | -4 | C. | 6 | D. | -6 |
分析 根据已知可得f(0)=0,进而求出k值,得到x≤0时,f(x)的解析式,先求出f(-ln5),进而可得答案.
解答 解:∵f(x)满足对?x∈R,f(-x)+f(x)=0,
故f(-x)=-f(x),
故f(0)=0
∵x≤0时,f(x)=$\frac{1}{{e}^{x}}$+k,
∴f(0)=1+k=0,
k=-1,
即x≤0时,f(x)=$\frac{1}{{e}^{x}}$-1,
则f(-ln5)=4=-f(ln5),
故f(ln5)=-4,
故选:B.
点评 本题考查的知识点是抽象函数及其应用,函数求值,难度中档.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
18.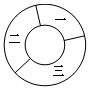 某游戏设计了如图所示的空心圆环形标靶,图中所标注的一、二、三区域所对的圆心角依次为$\frac{π}{2}$,$\frac{2π}{3}$,$\frac{5π}{6}$,则向该标靶内投点,该点落在区域二内的概率为( )
某游戏设计了如图所示的空心圆环形标靶,图中所标注的一、二、三区域所对的圆心角依次为$\frac{π}{2}$,$\frac{2π}{3}$,$\frac{5π}{6}$,则向该标靶内投点,该点落在区域二内的概率为( )
 某游戏设计了如图所示的空心圆环形标靶,图中所标注的一、二、三区域所对的圆心角依次为$\frac{π}{2}$,$\frac{2π}{3}$,$\frac{5π}{6}$,则向该标靶内投点,该点落在区域二内的概率为( )
某游戏设计了如图所示的空心圆环形标靶,图中所标注的一、二、三区域所对的圆心角依次为$\frac{π}{2}$,$\frac{2π}{3}$,$\frac{5π}{6}$,则向该标靶内投点,该点落在区域二内的概率为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{7}$ | D. | $\frac{3}{8}$ |
14.已知正三角形ABC的顶点A,B在抛物线y2=4x上,另一个顶点C(4,0),则这样的正三角形有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
18.已知角α终边上一点的坐标为P(sin$\frac{π}{10}$,cos$\frac{9π}{10}$),则角α是( )
| A. | $\frac{π}{10}$ | B. | $\frac{2π}{5}$ | C. | -$\frac{π}{10}$ | D. | -$\frac{2π}{5}$ |
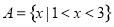 ,集合
,集合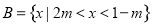 .
.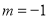 时,求
时,求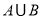 ;
;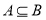 ,求实数
,求实数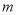 的取值范围;
的取值范围;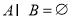 ,求实数
,求实数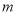 的取值范围.
的取值范围. 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PB⊥BC,PD⊥DC,且$PC=\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PB⊥BC,PD⊥DC,且$PC=\sqrt{3}$.