题目内容
已知
=(1,2),
=(-1,6),
=2
-
,求与
平行的单位向量的坐标.
| a |
| b |
| c |
| a |
| b |
| c |
考点:平面向量的坐标运算
专题:平面向量及应用
分析:直接求出
,然后求解与
平行的单位向量的坐标即可.
| c |
| c |
解答:
解:
=(1,2),
=(-1,6),
=2
-
=(3,-2).
与
平行的单位向量为:±
=±
(3,-2)=±(
,-
).
与
平行的单位向量的坐标(
,-
)或(-
,
)
| a |
| b |
| c |
| a |
| b |
与
| c |
| ||
|
|
| 1 | ||
|
3
| ||
| 13 |
2
| ||
| 13 |
与
| c |
3
| ||
| 13 |
2
| ||
| 13 |
3
| ||
| 13 |
2
| ||
| 13 |
点评:本题考查向量的平行与共线,单位向量的求法,基本知识的考查.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
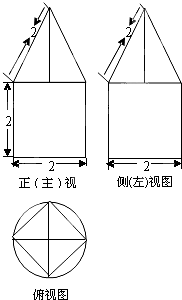 一空间几何体的三视图如图所示,则该几何体的表面积为( )
一空间几何体的三视图如图所示,则该几何体的表面积为( )A、6π+4
| ||||
B、6π+4
| ||||
C、2π+
| ||||
D、2π+4
|
给出下列结论:
①若
≠
,
•
=0,则
=
;
②若
•
=
•
,则
=
;
③(
•
)
=
(
•
);
④
,
为非零不共线,若|
+
|=|
-
|,则
⊥
;
⑤
,
,
非零不共线,则(
•
)•
-(
•
)•
与
垂直
其中正确的为( )
①若
| a |
| 0 |
| a |
| b |
| b |
| 0 |
②若
| a |
| b |
| b |
| c |
| a |
| c |
③(
| a |
| b |
| c |
| a |
| b |
| c |
④
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
⑤
| a |
| b |
| c |
| b |
| c |
| a |
| c |
| a |
| b |
| c |
其中正确的为( )
| A、②③ | B、①②④ | C、④⑤ | D、③④ |
已知某三棱锥的三视图均为腰长为2的等腰直角三角形(如图),则过该棱锥所有顶点的球的表面积为( )


| A、48π | B、24π |
| C、12π | D、8π |