题目内容
4.幂函数$f(x)=({m^2}-3m+3){x^{{m^2}-m-2}}$的图象与坐标轴没有公共点,则m的值为1或2.分析 根据幂函数的定义、图象与性质,列出方程组,即可求出m的值.
解答 解:幂函数$f(x)=({m^2}-3m+3){x^{{m^2}-m-2}}$的图象与坐标轴没有公共点,
∴$\left\{\begin{array}{l}{{m}^{2}-3m+3=1}\\{{m}^{2}-m-2≤0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=1或m=2}\\{-1≤m≤2}\end{array}\right.$,
即m=1或m=2.
故答案为:1或2.
点评 本题考查了幂函数的定义、图象与性质的应用问题,是基础题目.

练习册系列答案
相关题目
13.函数f(x)=$\frac{1}{2}$sin2x+$\frac{1}{2}$tan$\frac{π}{3}$cos2x的最小正周期为( )
| A. | $\frac{π}{2}$ | B. | π | C. | 2π | D. | 4π |
14.已知函数f(x)=$\left\{\begin{array}{l}{1+(\frac{1}{2})^{x},x<0}\\{\sqrt{x}+1,x≥0}\end{array}\right.$,则“x2-x-2>0”是“f(x)>3”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
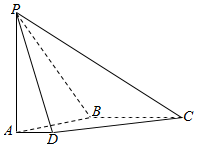 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AB⊥AD,AD∥BC,侧棱PA⊥底面ABCD,且PA=AB=BC=2,AD=1.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AB⊥AD,AD∥BC,侧棱PA⊥底面ABCD,且PA=AB=BC=2,AD=1.