题目内容
m是 时,不等式x2+mx+1≥0对任何x∈R都成立.
考点:函数恒成立问题
专题:函数的性质及应用
分析:不等式x2+mx+1≥0对于任意的x∈R均成立,只需△≤0即可求得m的取值范围.
解答:
解:∵x2+mx+1≥0对任何x∈R都成立,
∴△=m2-4≤0,
解得-2≤m≤2,
故当m∈[-2,2]时,不等式x2+mx+1≥0对任何x∈R都成立.
故答案为:m∈[-2,2]时
∴△=m2-4≤0,
解得-2≤m≤2,
故当m∈[-2,2]时,不等式x2+mx+1≥0对任何x∈R都成立.
故答案为:m∈[-2,2]时
点评:本题题考查二次函数在R中的恒成立问题,可以通过判别式法予以解决,也可以分离参数m,分类讨论解决.

练习册系列答案
相关题目
已知集合A={x|x2-3x+2=0},集合B={x|x>-1},则A∩B=( )
| A、(1,2) | B、{2} |
| C、{-1,2} | D、{1,2} |
已知约束条件
,且目标函数z=x-2y的最大值是4,则z的最小值是( )
|
| A、-2 | B、-7 | C、-3 | D、-5 |

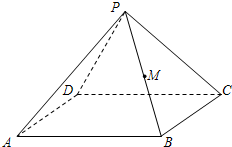 四棱锥P-ABCD中,棱长PD=a,底面ABCD是边长为a的菱形,点M为PB中点
四棱锥P-ABCD中,棱长PD=a,底面ABCD是边长为a的菱形,点M为PB中点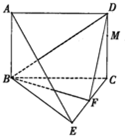 如图,平面ABCD⊥平面BCE,四边形ABCD为矩形,BC=CE,点F为CE的中点.
如图,平面ABCD⊥平面BCE,四边形ABCD为矩形,BC=CE,点F为CE的中点.