题目内容
14.已知角α的顶点在原点,始边与Ox轴重合,终边经过(4a,3a)(a<0),则下列计算正确的是( )| A. | sinα=$\frac{3}{5}$ | B. | cosα=$\frac{4}{5}$ | C. | tanα=-$\frac{3}{4}$ | D. | sinα=-$\frac{3}{5}$ |
分析 根据三角函数的定义建立方程关系进行求解即可.
解答 解:角α的顶点在原点,始边与Ox轴重合,终边经过P(4a,3a)(a<0),
∴r=|OP|=$\sqrt{(4a)^{2}+(3a)^{2}}$=5|a|=-5a,
则sinα=$\frac{3a}{-5a}$=-$\frac{3}{5}$,cosα=$\frac{4a}{-5a}$=-$\frac{4}{5}$,tanα=$\frac{3a}{4a}$=$\frac{3}{4}$,
故选:D.
点评 本题主要考查三角函数值的计算,利用三角函数的定义是解决本题的关键,比较基础.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
9.已知向量$\overrightarrow{a}$=(2,1),向量$\overrightarrow{b}$=(3,-4),若向量$λ\overrightarrow{a}$-$\overrightarrow{b}$与向量$\overrightarrow{a}+2\overrightarrow{b}$是共线向量,则实数λ的取值为( )
| A. | -$\frac{1}{2}$ | B. | -2 | C. | $\frac{1}{2}$ | D. | 2 |
19.sin50°cos35°+sin40°sin(-35°)=( )
| A. | $\frac{\sqrt{6}-\sqrt{2}}{4}$ | B. | $\frac{\sqrt{6}+\sqrt{2}}{4}$ | C. | $\frac{\sqrt{2}-\sqrt{6}}{4}$ | D. | $-\frac{\sqrt{6}+\sqrt{2}}{4}$ |
8.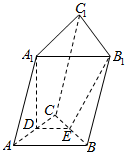 如图所示的三棱柱ABC-A1B1C1中,过A1B1的平面与平面ABC交于直线DE,则DE与AB的位置关系是( )
如图所示的三棱柱ABC-A1B1C1中,过A1B1的平面与平面ABC交于直线DE,则DE与AB的位置关系是( )
 如图所示的三棱柱ABC-A1B1C1中,过A1B1的平面与平面ABC交于直线DE,则DE与AB的位置关系是( )
如图所示的三棱柱ABC-A1B1C1中,过A1B1的平面与平面ABC交于直线DE,则DE与AB的位置关系是( )| A. | 异面 | B. | 平行 | C. | 相交 | D. | 以上均有可能 |
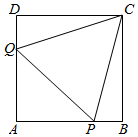 某地政府为提升城市形象,在该地区边长为1的正方形ABCD的空地建文化广场,在正方形ABCD的内部规划一块△CPQ区域种植花草,并满足P,Q分别为边AB,DA上的动点,且∠PCQ=$\frac{π}{3}$,问∠PCB多大时才能使△CPQ面积的最小,并求出最小值.
某地政府为提升城市形象,在该地区边长为1的正方形ABCD的空地建文化广场,在正方形ABCD的内部规划一块△CPQ区域种植花草,并满足P,Q分别为边AB,DA上的动点,且∠PCQ=$\frac{π}{3}$,问∠PCB多大时才能使△CPQ面积的最小,并求出最小值.