题目内容
6.设f(x)=$\frac{1-x}{1+x}$,记f1(x)=f(x),若fk+1(x)=f(fk(x)),k=1,2,…,则f2016(x)=x.分析 利用函数的性质推导出f1(x),f2(x),f3(x),f4(x),由此能求出f2016(x).
解答 解:∵f(x)=$\frac{1-x}{1+x}$,记f1(x)=f(x),fk+1(x)=f(fk(x)),k=1,2,…,
∴f1(x)=f(x)=$\frac{1-x}{1+x}$,
f2(x)=f(f1(x))=f($\frac{1-x}{1+x}$)=$\frac{1-\frac{1-x}{1+x}}{1+\frac{1-x}{1+x}}$=x,
f3(x)=f(f2(x))=f(x)=$\frac{1-x}{1+x}$,
f4(x)=f(f3(x))=f(x)=$\frac{1-x}{1+x}$.
…
∴fn(x)=$\left\{\begin{array}{l}{\frac{1-x}{1+x},x为奇数}\\{x,x为偶数}\end{array}\right.$.
∴f2016(x)=x.
故答案为:x.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.如果实数x,y,满足条件$\left\{\begin{array}{l}{x-y+1≥0}\\{2x+y-2≥0}\\{x-1≤0}\end{array}\right.$,则z=1-$\frac{2}{2x+3y}$的最大值为( )
| A. | 1 | B. | $\frac{3}{4}$ | C. | 0 | D. | $\frac{4}{7}$ |
14.已知角α的顶点在原点,始边与Ox轴重合,终边经过(4a,3a)(a<0),则下列计算正确的是( )
| A. | sinα=$\frac{3}{5}$ | B. | cosα=$\frac{4}{5}$ | C. | tanα=-$\frac{3}{4}$ | D. | sinα=-$\frac{3}{5}$ |
11.某市为了“还城一片蓝天”,决定大力发展公共交通,市物价局举行地铁票价定价听证会,讨论地铁的价格与老百姓的承受能力.消费者代表为440名,市政府、工会、消保委代表是460名,其他是(专家、经营者等)是500名,用分层抽样的方法从中抽取70名代表进行抽样凋查,对地铁的“服务满意度”与“价格满意度”都分为五个等级:1级(很不满意);2级(不满意);3级(一般);4级(满意);5级(很满意),其统计结果如表(服务满意度为x,价格满意度为y).
(1)求市政府、工会、消保委代表抽取的人数;
(2)求“服务满意度”为3时的5个“价格满意度”数据的方差.
 | 价格满意度 | |||||
| 1 | 2 | 3 | 4 | 5 | ||
| 服务满意度 | 1 | 1 | 1 | 2 | 2 | 0 |
| 2 | 2 | 1 | 3 | 4 | 1 | |
| 3 | 3 | 7 | 8 | 8 | 4 | |
| 4 | 1 | 4 | 6 | 4 | 1 | |
| 5 | 0 | 1 | 2 | 3 | 1 | |
(2)求“服务满意度”为3时的5个“价格满意度”数据的方差.
3. 某市四所重点中学进行高二期中联考,共有5000名学生参加,为了了解数学学科的学习情况,现从中随机的抽取若干名学生在这次测试中的数学成绩,制成如下频率分布表:
某市四所重点中学进行高二期中联考,共有5000名学生参加,为了了解数学学科的学习情况,现从中随机的抽取若干名学生在这次测试中的数学成绩,制成如下频率分布表:
(1)根据上面的频率分布表,推出①,②,③,④处的数字分别为,3,0.025,0.1,1;
(2)在所给的坐标系中画出[80,150]上的频率分布直方图;
(3)根据题中的信息估计总体:
①120分及以上的学生人数;
②成绩在[126,150]中的概率.
 某市四所重点中学进行高二期中联考,共有5000名学生参加,为了了解数学学科的学习情况,现从中随机的抽取若干名学生在这次测试中的数学成绩,制成如下频率分布表:
某市四所重点中学进行高二期中联考,共有5000名学生参加,为了了解数学学科的学习情况,现从中随机的抽取若干名学生在这次测试中的数学成绩,制成如下频率分布表:| 分组 | 频数 | 频率 |
| [80,90) | ① | ② |
| [90,100) | 0.050 | |
| [100,110) | 0.200 | |
| [110,120) | 36 | 0.300 |
| [120,130) | 0.275 | |
| [130,140) | 12 | ③ |
| [140,150] | 0.050 | |
| 合计 | ④ |
(2)在所给的坐标系中画出[80,150]上的频率分布直方图;
(3)根据题中的信息估计总体:
①120分及以上的学生人数;
②成绩在[126,150]中的概率.
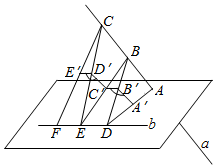 如图,直线a,b是异面直线,A,B,C为直线a上三点,D,E,F是直线b上三点,A′,B′,C′,D′,E′分别为AD,DB,BE,EC,CF的中点.
如图,直线a,b是异面直线,A,B,C为直线a上三点,D,E,F是直线b上三点,A′,B′,C′,D′,E′分别为AD,DB,BE,EC,CF的中点.