题目内容
15.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右顶点为A,若双曲线右支上存在两点B,C使得△ABC为等腰直角三角形,则该双曲线的离心率e的取值范围是( )| A. | (1,2) | B. | (2,+∞) | C. | (1,$\sqrt{2}$) | D. | ($\sqrt{2}$,+∞) |
分析 设其中一条渐近线与x轴的夹角为θ,由已知条件得tanθ<1,渐近线的方程为y=$\frac{b}{a}$x,从而$\frac{b}{a}$<1由此能求出该双曲线的离心率e的取值范围.
解答 解:如图,由△ABC为等腰直角三角形,所以∠BAx=45°,
设其中一条渐近线与x轴的夹角为θ,则θ<45°,即tanθ<1,
又上述渐近线的方程为y=$\frac{b}{a}$x,
则$\frac{b}{a}$<1,又e=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$,
∴1<e<$\sqrt{2}$,
双曲线的离心率e的取值范围(1,$\sqrt{2}$),
故选C.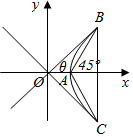
点评 本题考查双曲线的离心率的取值范围的求法,是中档题,解题时要认真审题,注意双曲线的性质的合理运用,属于中档题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目
8.已知i是虚数单位,复数z=(4+i)+(-3-2i)的虚部是( )
| A. | 1 | B. | $\sqrt{2}$ | C. | -1 | D. | -i |
10.已知集合A={x∈R||x|≤2},B={x∈Z|x2≤1},则A∩B=( )
| A. | [-1,1] | B. | [-2,2] | C. | {-1,0,1} | D. | {-2,-1,0,1,2} |
20.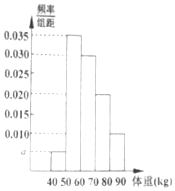 从某地高中男生中随机抽取100名同学,将他们的体重(单位:kg)数据绘制成频率分布直方图(如图),由直方图可知( )
从某地高中男生中随机抽取100名同学,将他们的体重(单位:kg)数据绘制成频率分布直方图(如图),由直方图可知( )
 从某地高中男生中随机抽取100名同学,将他们的体重(单位:kg)数据绘制成频率分布直方图(如图),由直方图可知( )
从某地高中男生中随机抽取100名同学,将他们的体重(单位:kg)数据绘制成频率分布直方图(如图),由直方图可知( )| A. | 估计体重的众数为50或60 | |
| B. | a=0.03 | |
| C. | 学生体重在[50,60)有35人 | |
| D. | 从这100名男生中随机抽取一人,体重在[60,80)的概率为$\frac{1}{3}$ |
7.已知函数f(x)=sin(2x+φ)($|φ|<\frac{π}{2}$)的图象沿x轴向左平移$\frac{π}{6}$个单位后关于y轴对称,则函数f(x)的一条对称轴是( )
| A. | $x=\frac{π}{12}$ | B. | $x=-\frac{π}{3}$ | C. | $x=-\frac{π}{6}$ | D. | $x=\frac{π}{3}$ |

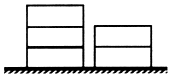 如图所示,某货场有两堆集装箱,一堆2个,一堆3个,现需要全部装运,每次只能从其中一堆取最上面的一个集装箱,则在装运的过程中不同取法的种数是( )
如图所示,某货场有两堆集装箱,一堆2个,一堆3个,现需要全部装运,每次只能从其中一堆取最上面的一个集装箱,则在装运的过程中不同取法的种数是( )