题目内容
10.设数列{an}的前n项和Sn=2an-a1,且a1+4是a2,a3的等差中项.(1)求数列{an}的通项公式;
(2)求数列$\left\{{\frac{n}{a_n}}\right\}$的前n项和Tn,求证:$\frac{1}{2}≤{T_n}<2$.
分析 (1)利用an=Sn-Sn-1(n>1)计算可知an=2an-1(n>1),进而可知数列{an}是首项为2、公比为2的等比数列,计算即得结论;
(2)通过(1)得$\frac{n}{a_n}=\frac{n}{2^n}$,进而利用错位相减法计算即得结论.
解答 解:(1)由已知Sn=2an-a1,有an=Sn-Sn-1=2an-2an-1(n>1),
即an=2an-1(n>1).------------------(2分)
从而a2=2a1,a3=4a1.
又因为a1+4是a2,a3的等差中项,即2(a1+4)=a2+a3.
解得a1=2.----------(3分)
所以数列{an}是首项为2,公比为2的等比数列.
故${a_n}={2^n}$…(4分)
(2)由(1)得$\frac{n}{a_n}=\frac{n}{2^n}$,所以${T_n}=\frac{1}{2}+\frac{2}{2^2}+\frac{3}{2^3}+…+\frac{n}{2^n}$,
$2{T_n}=1+1+\frac{3}{2^2}+…+\frac{n}{{{2^{n-1}}}}$,
两式相减${T_n}=1+\frac{1}{2}+\frac{1}{2^2}+…+\frac{1}{{{2^{n-1}}}}-\frac{n}{2^n}=\frac{{1-{{(\frac{1}{2})}^n}}}{{1-\frac{1}{2}}}-\frac{n}{2^n}=2-\frac{n+2}{2^n}$…(8分)
因为$\frac{n+2}{2^n}$-$\frac{n+3}{{{2^{n+1}}}}$=$\frac{n+1}{{{2^{n+1}}}}>0$,所以数列$\left\{{\frac{n+2}{2^n}}\right\}$递减…(10分)
即$0<\frac{n+2}{2^n}≤\frac{3}{2}$,从而$\frac{1}{2}≤{T_n}<2$…(12分)
点评 本题考查数列的通项及前n项和,考查错位相减法,注意解题方法的积累,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | {x|1<x<2} | B. | {x|1≤x<2} | C. | {x|x<2} | D. | {x|x≤1} |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | $\sqrt{5}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $\frac{{\sqrt{5}}}{2}$ |
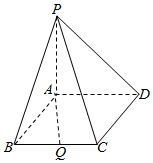 在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,四边形ABCD是菱形,并且PA=3,AB=2,∠ABC=60°,点Q为BC中点.
在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,四边形ABCD是菱形,并且PA=3,AB=2,∠ABC=60°,点Q为BC中点.