题目内容
11.某人有一容积为V,高为a且装满了油的直三棱柱形容器,不小心将该容器掉在地上,有两处破损并发生渗漏,其位置分别在两条侧棱上且距下底面高度分别为b、c的地方,且容器盖也被摔开了(盖为上底面),为减少油的损失,此人采用破口朝上,倾斜容器的方式拿回家,估计容器内的油最理想的剩余量是多少.(容器壁的厚度忽略不计)分析 如图所示,设直三棱柱的底面面积为S,则V=aS.当ADE平面为水平面时,容器内的油是最理想的剩余量.连接AB1,AC1.${V}_{A-{A}_{1}{B}_{1}{C}_{1}}$=$\frac{1}{3}$aS=$\frac{1}{3}V$.设${V}_{A-DE{C}_{1}{B}_{1}}$=V1,VA-BCED=V2.可得$\frac{{V}_{1}}{{V}_{2}}$=$\frac{{S}_{DE{C}_{1}{B}_{1}}}{{S}_{BCED}}$=$\frac{b+c}{a-c+a-b}$,${V}_{1}+{V}_{2}=\frac{2}{3}V$,解出V1即可得出.
解答 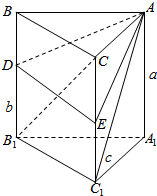 解:如图所示,
解:如图所示,
设直三棱柱的底面面积为S,则V=aS.
当ADE平面为水平面时,容器内的油是最理想的剩余量.
连接AB1,AC1.
${V}_{A-{A}_{1}{B}_{1}{C}_{1}}$=$\frac{1}{3}$aS=$\frac{1}{3}V$.
设${V}_{A-DE{C}_{1}{B}_{1}}$=V1,VA-BCED=V2.
则$\frac{{V}_{1}}{{V}_{2}}$=$\frac{{S}_{DE{C}_{1}{B}_{1}}}{{S}_{BCED}}$=$\frac{b+c}{a-c+a-b}$,${V}_{1}+{V}_{2}=\frac{2}{3}V$,
解得V1=$\frac{b+c}{3a}V$.
∴V1+${V}_{A-{A}_{1}{B}_{1}{C}_{1}}$=$\frac{b+c}{3a}V$+$\frac{1}{3}V$=$\frac{a+b+c}{3a}V$.
因此,容器内的油的最理想的剩余量是$\frac{a+b+c}{3a}V$.
点评 本题考查了空间位置关系、分割计算体积,考查了空间想象能力、推理能力与计算能力,属于中档题.

| A. | -3+4i | B. | 0 | C. | -4+3i | D. | -4-3i |
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要条件 | D. | 既不充分也不必要 |

 如图,在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点M(1,$\frac{\sqrt{2}}{2}$),离心率e=$\frac{\sqrt{2}}{2}$,F1、F2为椭圆的左、右焦点.
如图,在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点M(1,$\frac{\sqrt{2}}{2}$),离心率e=$\frac{\sqrt{2}}{2}$,F1、F2为椭圆的左、右焦点. 已知直线l1:4x-3y+6=0和直线l2:x=0,抛物线y2=4x上一动点P到直线l1和直线l2的距离之和的最小值是( )
已知直线l1:4x-3y+6=0和直线l2:x=0,抛物线y2=4x上一动点P到直线l1和直线l2的距离之和的最小值是( )