题目内容
10.以下命题正确的是:①③④.①把函数y=3sin(2x+$\frac{π}{3}$)的图象向右平移$\frac{π}{6}$个单位,可得到y=3sin2x的图象;
②四边形ABCD为长方形,AB=2,BC=1,O为AB中点,在长方形ABCD内随机取一点P,取得的P点到O的距离大于1的概率为1-$\frac{π}{2}$;
③某校开设A类选修课3门,B类选择课4门,一位同学从中共选3门,若要求两类课程中各至少选一门,则不同的选法共有30种;
④在某项测量中,测量结果ξ服从正态分布N(2,σ2)(σ>0).若ξ在(-∞,1)内取值的概率为0.1,则ξ在(2,3)内取值的概率为0.4.
分析 ①根据三角函数的图象平移关系进行判断.
②根据几何概型的概率公式进行判断.
③根据排列组合的计数原理进行判断.
④根据正态分布的概率关系进行判断.
解答 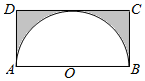 解:①把函数y=3sin(2x+$\frac{π}{3}$)的图象向右平移$\frac{π}{6}$个单位,得到y=3sin[2(x-$\frac{π}{6}$)+$\frac{π}{3}$]=3sin(2x-$\frac{π}{3}$+$\frac{π}{3}$)=3sin2x,即可得到y=3sin2x的图象;故①正确,
解:①把函数y=3sin(2x+$\frac{π}{3}$)的图象向右平移$\frac{π}{6}$个单位,得到y=3sin[2(x-$\frac{π}{6}$)+$\frac{π}{3}$]=3sin(2x-$\frac{π}{3}$+$\frac{π}{3}$)=3sin2x,即可得到y=3sin2x的图象;故①正确,
解:已知如图所示:长方形面积为2,以O为圆心,1为半径作圆,在矩形内部的部分(半圆)面积为 $\frac{π}{2}$,
因此取到的点到O的距离大于1的概率P=$\frac{2-\frac{π}{2}}{2}$=1-$\frac{π}{4}$;故②错误;
③可分以下2种情况:(1)A类选修课选1门,B类选修课选2门,有C31C42种不同的选法;
(2)A类选修课选2门,B类选修课选1门,有C32C41种不同的选法.
∴根据分类计数原理知不同的选法共有C31C42+C32C41=18+12=30种.故要求两类课程中各至少选一门,则不同的选法共有30种正确,故③正确,
④在某项测量中,测量结果ξ服从正态分布N(2,σ2)(σ>0).则正态曲线关于x=2对称,
若ξ在(-∞,1)内取值的概率为0.1,则ξ在[1,2]的概率P(1<x<2)=0.5-0.=4,
则在(2,3)内取值的概率P(2<x<3)=P(1<x<2)=0.4.故④正确,
故答案为:①③④
点评 本题主要考查命题的真假判断,涉及的知识点较多,综合性较强,但难度不是很大.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
1.△ABC中,AB=2,AC=3,∠B=60°,则cosC=( )
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $±\frac{{\sqrt{6}}}{3}$ | C. | $-\frac{{\sqrt{6}}}{3}$ | D. | $\frac{{\sqrt{6}}}{3}$ |
2.设函数$f(x)=\left\{{\begin{array}{l}{{x^2}-4}&{x>0}\\{2x}&{x≤0}\end{array}}\right.$,则f[f(1)]的值为( )
| A. | -6 | B. | 0 | C. | 4 | D. | 5 |
 某商店根据以往某种玩具的销售纪录,绘制了日销售量的频率分布直方图,如图所示.,将日销售量落入各组的频率视为概率,并假设每天的销售量互相独立.
某商店根据以往某种玩具的销售纪录,绘制了日销售量的频率分布直方图,如图所示.,将日销售量落入各组的频率视为概率,并假设每天的销售量互相独立.