题目内容
10.已知a<0,解关于x的不等式ax2+(2-a)x-2>0.分析 不等式可因式分解为(ax+1)(x-1)>0,
由a<0,左右两边同时除以a,得$[{x-(-\frac{1}{a})}](x-1)<0$,
进而讨论$-\frac{1}{a}$和1的大小,写出对应的解集.
解答 解:不等式ax2+(2-a)x-2>0可化为(ax+1)(x-1)>0,
∵a<0,左右两边同时除以a,得
$[{x-(-\frac{1}{a})}](x-1)<0$,
比较$-\frac{1}{a}$和1的大小,得:
①当-1<a<0时,∵$-\frac{1}{a}>1$,且原不等式可化为$[{x-(-\frac{1}{a})}](x-1)<0$,
∴其解集为$\left\{{x|1<x<-\frac{1}{a}}\right\}$;
②当a=-1时,∵$1=-\frac{1}{a}$,且原不等式可化为(x-1)2<0,其解集为∅;
③当a<-1时,∵$1>-\frac{1}{a}$,且原不等式可化为$[{x-(-\frac{1}{a})}](x-1)<0$,
∴其解集为$\left\{{x|-\frac{1}{a}<x<1}\right\}$;
综上:当-1<a<0时,解集为$\left\{{x|1<x<-\frac{1}{a}}\right\}$;
当时a=-1,解集为∅;
当a<-1时,解集为$\left\{{x|-\frac{1}{a}<x<1}\right\}$.
点评 本题考查了用分类讨论法求含有字母系数的一元二次不等式的问题,是基础题目.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目
1.在空间直角坐标系中,点A(1,0,1)与点B(2,1,-1)间的距离为( )
| A. | $\sqrt{3}$ | B. | 3 | C. | $\sqrt{6}$ | D. | $\frac{{\sqrt{6}}}{2}$ |
18.已知A(3,0),B(0,4),△AOB绕y轴旋转一周得到的几何体的表面积和体积分别是( )
| A. | 9π,12π | B. | 12π,9π | C. | 24π,12π | D. | 15π,36π |
5.中央电视台为了调查近三年的春晚节目中各类节目的受欢迎程度,用分层抽样的方法,从2014年至2016年春晚的50个歌舞类节目,40个戏曲类节目,30个小品类节目中抽取样本进行调查,若样本中的歌舞类和戏曲类节目共有27个,则样本容量为( )
| A. | 36 | B. | 35 | C. | 32 | D. | 30 |
2.设实数x,y满足条件$\left\{\begin{array}{l}{x-y+2≥0}\\{2x-y-4≤0}\\{x≥0,y≥0}\end{array}\right.$,若目标函数z=ax+by(a>0,b>0)的最大值为 12,则$\frac{3}{a}$+$\frac{4}{b}$的最小值为( )
| A. | $\frac{49}{6}$ | B. | $\frac{25}{6}$ | C. | $\frac{8}{3}$ | D. | 4 |
11.已知奇函数f(x)的定义域为(-∞,0)∪(0,+∞),且不等式$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$>0对任意两个不相等的正实数x1,x2都成立,在下列不等式中,正确的是( )
| A. | f(-5)>f(3) | B. | f(-5)<f(3) | C. | f(-3)>f(-5) | D. | f(-3)<f(-5) |
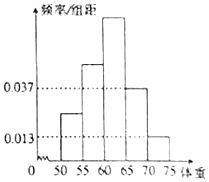 为了解今年某校高三毕业班想参军的学生体重情况,将所得的数据整理后,画出了频率分布直方图(如图).已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为24.
为了解今年某校高三毕业班想参军的学生体重情况,将所得的数据整理后,画出了频率分布直方图(如图).已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为24.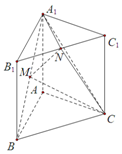 如图,直三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,AA1=2,点M,N分别为A1B和B1C1的中点.
如图,直三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,AA1=2,点M,N分别为A1B和B1C1的中点.