题目内容
2．已知三棱锥P-ABC的四个顶点都在球O的表面上，且PA=PB=PC=2$\sqrt{5}$，若平面ABC被球O截得的截面面积为16π，则球O的表面积为100π．分析 先确定平面ABC被球O截得的截面圆的半径，进而求得正三棱锥的高，再利用勾股定理，求得外接球的半径，即可求得外接球的表面积．
解答 解：∵平面ABC被球O截得的截面面积为16π，
∴截面圆的半径r=4，
△ABC的边长为：4$\sqrt{3}$，
则P到平面ABC的距离d=$\sqrt{{（2\sqrt{5}）}^{2}-{4}^{2}}$=2，
设外接球的半径为R，则R2=42+（R-2）2，
∴R=5，
∴外接球的表面积为4πR2=100π，
故答案为：100π．
点评 本题考查正三棱锥的外接球的表面积，考查学生的计算能力，正确运用正三棱锥的性质是关键．
练习册系列答案
相关题目
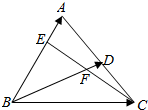如图，在△ABC中，D为AC的中点，E是AB上的点，且$\frac{AE}{EB}$=$\frac{1}{2}$，CE和BD交于点F，设$\overrightarrow{BD}$=$\overrightarrow{a}$，$\overrightarrow{BA}$=$\overrightarrow{b}$．
12．设点A（3，3，1），B（1，0，5），C（0，1，0），则线段AB的中点与点C的距离为（ ）
| A． | $\frac{\sqrt{13}}{4}$ | B． | $\frac{\sqrt{13}}{2}$ | C． | $\frac{\sqrt{53}}{4}$ | D． | $\frac{\sqrt{53}}{2}$ |