已知正整数a.b.c满足a＜b＜c.若函数φ(x)=|x-a|+|x-b|+|x-c|的图象与函数y=-2x+2015的图象有且仅有一个公共点.则正整数c的最小值是1008．题目和参考答案——青夏教育精英家教网——

题目内容

2．已知正整数a，b，c满足a＜b＜c，若函数φ（x）=|x-a|+|x-b|+|x-c|的图象与函数y=-2x+2015的图象有且仅有一个公共点，则正整数c的最小值是1008．

分析化简并作出φ（x）=|x-a|+|x-b|+|x-c|与函数y=-2x+2015的图象，从而可得b+c-2a=2015-2a，从而解得．

解答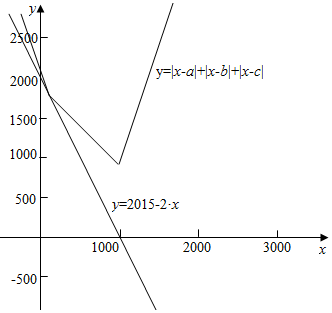解：φ（x）=|x-a|+|x-b|+|x-c|
=$\left\{\begin{array}{l}{a+b+c-3x，x≤a}\\{b+c-a-x，a＜x≤b}\\{c-a-b+x，b＜x≤c}\\{3x-a-b-c，x＞c}\end{array}\right.$，
作φ（x）=|x-a|+|x-b|+|x-c|与函数y=-2x+2015的图象如右图，
结合图象可知，
若使两函数的图象有且仅有一个公共点，
则b+c-2a=2015-2a，
故b+c=2015，
又∵a＜b＜c，且都是正整数，
∴c的最小值为1008，
故答案为：1008．

点评本题考查了线性规划的变形应用及数形结合的思想方法应用，属于中档题．

练习册系列答案

西城学科专项测试系列答案

小考必做系列答案

小考实战系列答案

小考复习精要系列答案

小考总动员系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

相关题目

12．已知函数f（x）=cos2x+cos²x，求
（1）周期；
（2）当x∈[$\frac{π}{6}$，$\frac{2π}{3}$]，求值域．

13．已知数列{a_n}中，a₁=1，a₂=$\frac{2}{3}$，$\frac{1}{{a}_{n-2}}+\frac{1}{{a}_{n}}=\frac{2}{{a}_{n-1}}$（n∈N^*，n≥3），求a₃，a₄．

10．已知函数f（x）=x²+3x，则f（3）与f（$\frac{1}{3}$）的积为8．

17．已知$\overrightarrow{a}$=（x+y+1，2x-y），$\overrightarrow{b}$=（x-y，x+2y-2），若2$\overrightarrow{a}$=3$\overrightarrow{b}$，求x、y的值．

5．若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的一条渐近线过曲线y=x²-4x+1的最低点，则该双曲线的离心率e的值是（　　）

$\frac{\sqrt{15}}{3}$

$\frac{\sqrt{13}}{3}$

$\frac{\sqrt{13}}{2}$

$\frac{\sqrt{15}}{2}$

A，B两地之间隔着一个水塘（如图所示），现选择另一点C，测得CA=182m，CB=126m，∠ACB=60°，求A，B两地之间的距离．

9．已知函数f（x）=Asin（ωx+φ）+m的最小值是0，最大值是4，最小正周期是$\frac{π}{2}$，其图象的一条对称轴是x=$\frac{π}{3}$，则函数f（x）的解析式应为（　　）

f（x）=Asin（4x+$\frac{π}{6}$）

f（x）=2sin（2x+$\frac{π}{3}$）+2

f（x）=sin（4x+$\frac{π}{3}$）+2

f（x）=2sin（4x+$\frac{π}{6}$）+2

10．若方程x²+（1-k）x-2（k+1）=0的一个根在区间（2，3）内，则实数k的取值范围是（　　）