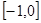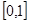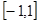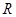题目内容
(本题满分12分)
已知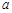 为实数,
为实数,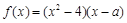 ,
,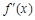 为
为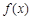 的导函数.
的导函数.
(1)求导数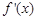 ;
;
(2)若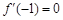 ,求
,求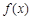 在
在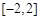 上的最大值和最小值;
上的最大值和最小值;
(3)若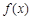 在
在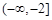 和
和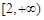 上都是递增的,求
上都是递增的,求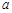 的取值范围.
的取值范围.
已知
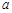 为实数,
为实数,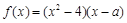 ,
,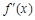 为
为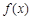 的导函数.
的导函数.(1)求导数
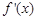 ;
;(2)若
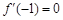 ,求
,求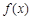 在
在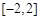 上的最大值和最小值;
上的最大值和最小值;(3)若
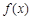 在
在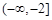 和
和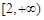 上都是递增的,求
上都是递增的,求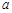 的取值范围.
的取值范围.(1)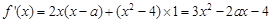 .
.
(2) 在
在 上的最大值为
上的最大值为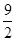 ,最小值为
,最小值为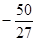 .
.
(3)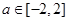 .
.
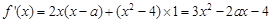 .
.(2)
 在
在 上的最大值为
上的最大值为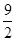 ,最小值为
,最小值为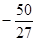 .
.(3)
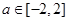 .
.本试题主要是考查了导数的几何意义的运用和导数在研究函数最值的思想的运用,和利用单调性,逆向求解参数的取值范围的综合运用。
(1)主要是考查了初等函数的导数的计算。
(2)由由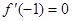 ,得
,得 得到解析式,然后确定解析式后再求解导数,分析函数的单调性,得到最值。
得到解析式,然后确定解析式后再求解导数,分析函数的单调性,得到最值。
(3)如果函数在给定区间单调递增,说明在该区间导数值恒大于等于零,分离参数的思想求解得到。
解:(1)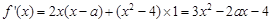 .
.
(2) ,
,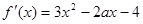 .
.
由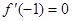 ,得
,得 ,此时
,此时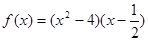 ,
, ,
,
由 ,得
,得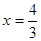 或
或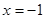 .
.
又 ,
, ,
, ,
,

 在
在 上的最大值为
上的最大值为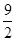 ,最小值为
,最小值为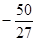 .
.
(3)解法一
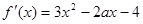 ,
,
依题意: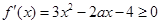 对
对 恒成立,即
恒成立,即
 ,所以
,所以
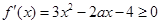 对
对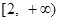 恒成立,即
恒成立,即
 ,所以
,所以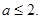
综上: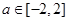 .
.
解法二
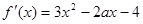 ,
,
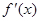 的图像是开口向上且过点
的图像是开口向上且过点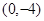 的抛物线,由条件得
的抛物线,由条件得 ,
, ,
,
 ,
,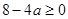 .解得
.解得 .
. 
 的取值范围为
的取值范围为 .
.
(1)主要是考查了初等函数的导数的计算。
(2)由由
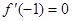 ,得
,得 得到解析式,然后确定解析式后再求解导数,分析函数的单调性,得到最值。
得到解析式,然后确定解析式后再求解导数,分析函数的单调性,得到最值。(3)如果函数在给定区间单调递增,说明在该区间导数值恒大于等于零,分离参数的思想求解得到。
解:(1)
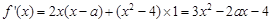 .
.(2)
 ,
,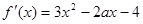 .
.由
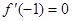 ,得
,得 ,此时
,此时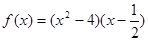 ,
, ,
,由
 ,得
,得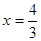 或
或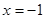 .
.又
 ,
, ,
, ,
,
 在
在 上的最大值为
上的最大值为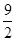 ,最小值为
,最小值为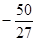 .
.(3)解法一

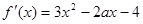 ,
,依题意:
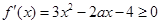 对
对 恒成立,即
恒成立,即 ,所以
,所以
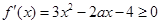 对
对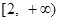 恒成立,即
恒成立,即 ,所以
,所以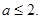
综上:
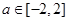 .
.解法二

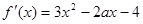 ,
,
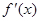 的图像是开口向上且过点
的图像是开口向上且过点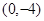 的抛物线,由条件得
的抛物线,由条件得 ,
, ,
, ,
,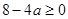 .解得
.解得 .
. 
 的取值范围为
的取值范围为 .
.
练习册系列答案
相关题目
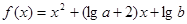 满足
满足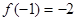 且对于任意
且对于任意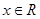 , 恒有
, 恒有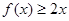 成立
成立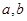 的值; (2)解不等式
的值; (2)解不等式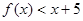
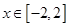 时,函数
时,函数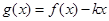 是单调函数,求实数
是单调函数,求实数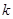 的取值范围。
的取值范围。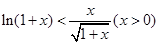
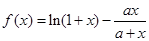 在
在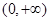 上单调递增,求实数
上单调递增,求实数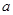 的取值范围.
的取值范围.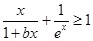 在
在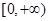 上恒成立,求实数
上恒成立,求实数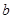 的最大值.
的最大值.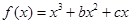 的导函数的图象关于直线x=2对称.
的导函数的图象关于直线x=2对称.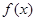 在
在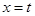 处取得极小值,记此极小值为
处取得极小值,记此极小值为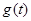 ,求
,求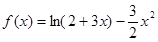 .
.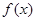 在[0,1]上的极值;
在[0,1]上的极值;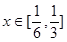 ,不等式
,不等式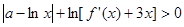 成立,求实数
成立,求实数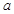 的取值范围;
的取值范围;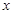 的方程
的方程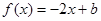 在[0,1]上恰有两个不同的实根,求实数
在[0,1]上恰有两个不同的实根,求实数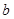 的取值范围.
的取值范围.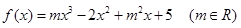 且
且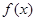 在
在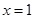 处取得极小值
处取得极小值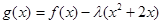 在
在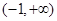 上是增函数,求实数
上是增函数,求实数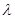 的取值范围。
的取值范围。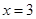 是函数
是函数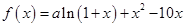 的一个极值点.
的一个极值点.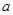 ;
;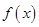 的单调区间;
的单调区间;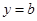 与函数
与函数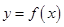 的图象有3个交点,求
的图象有3个交点,求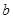 的取值范围.
的取值范围.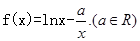
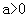 ,试判断函数
,试判断函数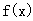 在定义域内的单调性;
在定义域内的单调性;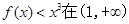 上恒成立,求实数
上恒成立,求实数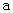 的取值范围。
的取值范围。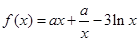 .
.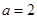 时,求函数
时,求函数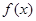 的最小值;
的最小值;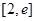 上单调递增,求实数
上单调递增,求实数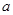 的取值范围.
的取值范围.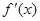 是函数
是函数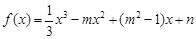 的导函数,若函数
的导函数,若函数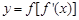 在区间
在区间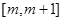 上单调递减,则实数
上单调递减,则实数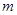 的取值范围是( )
的取值范围是( )