题目内容
5.与y=|x|为同一函数的是( )| A. | $y={(\sqrt{x})^2}$ | B. | $y=\sqrt{x^2}$ | C. | $y=\left\{\begin{array}{l}x,(x>0)\\-x,(x<0)\end{array}\right.$ | D. | $y=\frac{x^2}{x}$ |
分析 根据两个函数的定义域相同,对应关系也相同,即可判断它们的同一函数.
解答 解:对于A,函数y=${(\sqrt{x})}^{2}$=x(x≥0),与y=|x|(x∈R)的定义域不同,对应关系也不同,所以不是同一函数;
对于B,函数y=$\sqrt{{x}^{2}}$=|x|(x∈R),与y=|x|(x∈R)的定义域相同,对应关系也相同,所以是同一函数;
对于C,函数y=$\left\{\begin{array}{l}{x,x>0}\\{-x,x<0}\end{array}\right.$=|x|(x≠0),与y=|x|(x∈R)的定义域不同,所以不是同一函数;
对于D,函数y=$\frac{{x}^{2}}{x}$=x(x≠0),与y=|x|(x∈R)的定义域不同,对应关系也不同,所以不是同一函数.
故选:B.
点评 本题考查了判断两个函数是否为同一函数的应用问题,是基础题目.

练习册系列答案
相关题目
15.已知点(a,b)与点(2,0)位于直线2x+3y-1=0的同侧,且a>0,b>0,则z=a+2b的取值范围是( )
| A. | $(\frac{1}{2},\frac{2}{3})$ | B. | $(-∞,\frac{1}{2})$ | C. | $(\frac{1}{2},+∞)$ | D. | $(\frac{2}{3},+∞)$ |
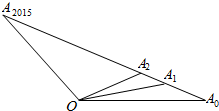 如图,O为直线A0A2015外一点,若A0,A1,A2,A3,A4,A5,…,A2015中任意相邻两点的距离相等,设$\overrightarrow{O{A}_{0}}$=$\overrightarrow{a}$,$\overrightarrow{O{A}_{2015}}$=$\overrightarrow{b}$,用$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{O{A}_{0}}$+$\overrightarrow{O{A}_{1}}$+…+$\overrightarrow{O{A}_{2015}}$,其结果为1008($\overrightarrow{a}$+$\overrightarrow{b}$).
如图,O为直线A0A2015外一点,若A0,A1,A2,A3,A4,A5,…,A2015中任意相邻两点的距离相等,设$\overrightarrow{O{A}_{0}}$=$\overrightarrow{a}$,$\overrightarrow{O{A}_{2015}}$=$\overrightarrow{b}$,用$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{O{A}_{0}}$+$\overrightarrow{O{A}_{1}}$+…+$\overrightarrow{O{A}_{2015}}$,其结果为1008($\overrightarrow{a}$+$\overrightarrow{b}$).