题目内容
20.若实数x,y满足不等式组$\left\{\begin{array}{l}{x+y-4≤0}\\{2x-3y-8≤0}\\{x≥1}\end{array}\right.$,目标函数z=kx-y的最大值为12,最小值为0,则实数k=3.分析 先画出可行域,得到角点坐标.利用k与0的大小,分类讨论,结合目标函数的最值求解即可.
解答  解:实数x,y满足不等式组$\left\{\begin{array}{l}{x+y-4≤0}\\{2x-3y-8≤0}\\{x≥1}\end{array}\right.$的可行域如图:得:A(1,3),B(1,-2),C(4,0).
解:实数x,y满足不等式组$\left\{\begin{array}{l}{x+y-4≤0}\\{2x-3y-8≤0}\\{x≥1}\end{array}\right.$的可行域如图:得:A(1,3),B(1,-2),C(4,0).
①当k=0时,目标函数z=kx-y的最大值为12,最小值为0,不满足题意.
②当k>0时,目标函数z=kx-y的最大值为12,最小值为0,当直线z=kx-y过C(4,0)时,Z取得最大值12.
当直线z=kx-y过A(1,3)时,Z取得最小值0.
可得k=3,满足题意.
③当k<0时,目标函数z=kx-y的最大值为12,最小值为0,当直线z=kx-y过C(4,0)时,Z取得最大值12.可得k=-3,
当直线z=kx-y过,B(1,-2)时,Z取得最小值0.可得k=-2,
无解.
综上k=3
故答案为:3.
点评 本题主要考查简单线性规划以及分类讨论思想.解决本题计算量较大.属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.定义域为R的函数f(x)满足:f(x+2)=2f(x),当x∈[0,2)时,$f(x)=\left\{\begin{array}{l}{x^2}-x,x∈[0,1)\\-{(\frac{1}{2})^{|x-\frac{3}{2}|}},x∈[1,2)\end{array}\right.$,若x∈[-4,-2)时,$f(x)≥\frac{1}{4}-\frac{1}{2t}$恒成立,则实数t的取值范围是( )
| A. | $(0,\frac{2}{5}]$ | B. | $(0,\frac{2}{3}]$ | C. | (0,1] | D. | (0,2] |
11.在△ABC中,|AB|=5,|AC|=6,若B=2C,则边BC的长为( )
| A. | 5 | B. | $\frac{11}{5}$ | C. | $\frac{9}{5}$ | D. | $\frac{7}{5}$ |
5.点M(3,2)到拋物线C:y=ax2(a>0)准线的距离为4,F为拋物线的焦点,点N(l,l),当点P在直线l:x-y=2上运动时,$\frac{|PN|-1}{|PF|}$的最小值为( )
| A. | $\frac{3-2\sqrt{2}}{8}$ | B. | $\frac{2-\sqrt{2}}{4}$ | C. | $\frac{5-2\sqrt{2}}{8}$ | D. | $\frac{5-2\sqrt{2}}{4}$ |
10.在区间[0,$\frac{π}{2}$]上随机地取一个数x,则事件“$\frac{1}{2}$≤sin x≤$\frac{{\sqrt{3}}}{2}$”发生的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
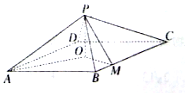 如图,四棱锥P-ABCD中,底面是以O为中心的菱形,PO⊥底面$ABCD,AB=2,∠BAD=\frac{π}{3},M$为BC上一点,且$BM=\frac{1}{2}$.
如图,四棱锥P-ABCD中,底面是以O为中心的菱形,PO⊥底面$ABCD,AB=2,∠BAD=\frac{π}{3},M$为BC上一点,且$BM=\frac{1}{2}$.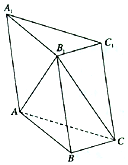 如图所示,已知三棱柱ABC-A1B1C1中,A1C1=B1C1,A1A=A1B1,∠AA1B1=60°.
如图所示,已知三棱柱ABC-A1B1C1中,A1C1=B1C1,A1A=A1B1,∠AA1B1=60°. 某校高三文科班150名男生在“学生体质健康50米跑”单项测试中,成绩全部介于6秒与11秒之间.现将测试结果分成五组:第一组[6,7];第二组(7,8],…,第五组(10,11].如图是按上述分组方法得到的频率分布直方图.按国家标准,高三男生50米跑成绩小于或等于7秒认定为优秀,若已知第四组共48人,则该校文科班男生在这次测试中成绩优秀的人数是9.
某校高三文科班150名男生在“学生体质健康50米跑”单项测试中,成绩全部介于6秒与11秒之间.现将测试结果分成五组:第一组[6,7];第二组(7,8],…,第五组(10,11].如图是按上述分组方法得到的频率分布直方图.按国家标准,高三男生50米跑成绩小于或等于7秒认定为优秀,若已知第四组共48人,则该校文科班男生在这次测试中成绩优秀的人数是9.