题目内容
12.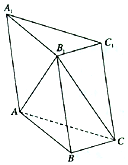 如图所示,已知三棱柱ABC-A1B1C1中,A1C1=B1C1,A1A=A1B1,∠AA1B1=60°.
如图所示,已知三棱柱ABC-A1B1C1中,A1C1=B1C1,A1A=A1B1,∠AA1B1=60°.(1)求证:AB⊥B1C;
(2)若A1B1=B1C=2,${B_1}{C_1}=\sqrt{2}$,求二面角C1-AB1-B的余弦值.
分析 (1)推导出AB⊥OB1,AB⊥OC,从而AB⊥平面OCB1,由此能证明AB⊥B1C.
(2)以O为原点,OB,OC,OB1方向为x,y,z轴的正向,建立空间直角坐标系,利用向量法能求出二面角C1-AB1-B的余弦值.
解答 证明:(1)∵四边形AA1B1B为平行四边形,且A1A=A1B1,∠AA1B1=60°,
∴△ABB1为等边三角形,
取AB中点O,连接OC,OB1,则AB⊥OB1,
∵CA=CB,∴AB⊥OC,
∵OC∩OB1=O,OB1?平面OB1C,OC?平面OB1C,
∴AB⊥平面OCB1,∴AB⊥B1C.
解:(2)∵△ABB1为等边三角形,AB=2,∴$O{B_1}=\sqrt{3}$,
∵在△ABC中,AB=2,$BC=AC=\sqrt{2}$,O为AB中点,
∴OC=1,
∵B1C=2,$O{B_1}=\sqrt{3}$,∴$O{B_1}^2+O{C^2}={B_1}{C^2}$,
∴OB1⊥OC,
又OB1⊥AB,
∴OB1⊥平面ABC.
以O为原点,OB,OC,OB1方向为x,y,z轴的正向,建立如图所示的坐标系,
A(-1,0,0),${B_1}(0,0,\sqrt{3})$,B(1,0,0),C(0,1,0),
则$\overrightarrow{O{C_1}}=\overrightarrow{OC}+\overrightarrow{C{C_1}}=\overrightarrow{OC}+\overrightarrow{B{B_1}}=(-1,1,\sqrt{3})$,
则${C_1}(-1,1,\sqrt{3})$,$\overrightarrow{A{B_1}}=(1,0,\sqrt{3})$,$\overrightarrow{A{C_1}}=(0,1,\sqrt{3})$,
则平面BAB1的一个法向量$\overrightarrow m=(0,1,0)$,
设$\overrightarrow n=(x,y,z)$为平面AB1C1的法向量,
则$\left\{\begin{array}{l}\overrightarrow n•\overrightarrow{A{B_1}}=x+\sqrt{3}z=0\\ \overrightarrow n•\overrightarrow{A{C_1}}=y+\sqrt{3}z=0\end{array}\right.$令z=-1,∴$x=y=\sqrt{3}$,
∴$\overrightarrow n=(\sqrt{3},\sqrt{3},-1)$,
∴$cos<\overrightarrow m,\overrightarrow n>=\frac{\overrightarrow m•\overrightarrow n}{|\overrightarrow m|•|\overrightarrow n|}=\frac{{\sqrt{21}}}{7}$.
由图形知二面角C1-AB1-B是锐角,
∴二面角C1-AB1-B的余弦值为$\frac{\sqrt{21}}{7}$.
点评 本题考查线线垂直的证明,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注空间思维能力的培养.

 名校课堂系列答案
名校课堂系列答案| A. | 40 | B. | 36 | C. | 32 | D. | 24 |
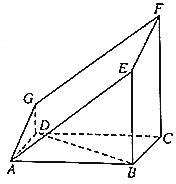 如图所示的多面体是由一个直平行六面体被平面AEFG所截后得到的,其中∠BAE=∠GAD=45°,AB=2AD=2,∠BAD=60°.
如图所示的多面体是由一个直平行六面体被平面AEFG所截后得到的,其中∠BAE=∠GAD=45°,AB=2AD=2,∠BAD=60°. 如图,已知四棱锥P-ABCD中,底面ABCD是菱形,PD⊥平面ABCD,E为PB上任意一点.
如图,已知四棱锥P-ABCD中,底面ABCD是菱形,PD⊥平面ABCD,E为PB上任意一点.