题目内容
10.在区间[0,$\frac{π}{2}$]上随机地取一个数x,则事件“$\frac{1}{2}$≤sin x≤$\frac{{\sqrt{3}}}{2}$”发生的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
分析 首先求出在区间[0,$\frac{π}{2}$]上满足“$\frac{1}{2}$≤sin x≤$\frac{{\sqrt{3}}}{2}$”的x范围,利用区间长度比求事件发生的概率.
解答 解:在区间[0,$\frac{π}{2}$]上满足“$\frac{1}{2}$≤sin x≤$\frac{{\sqrt{3}}}{2}$”的x范围为[$\frac{π}{6},\frac{π}{3}$],由几何概型的公式得到,事件发生的概率为$\frac{\frac{π}{3}-\frac{π}{6}}{\frac{π}{2}}=\frac{1}{3}$;
故选B.
点评 本题考查了几何概型的概率求法;关键是明确几何测度为区间的长度.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目
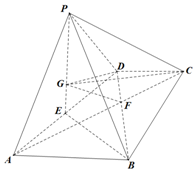 如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,底面ABCD为梯形,AB∥CD,AB=2DC=2$\sqrt{3}$,AC∩BD=F.且△PAD与△ABD均为正三角形,E为AD的中点,G为△PAD重心.
如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,底面ABCD为梯形,AB∥CD,AB=2DC=2$\sqrt{3}$,AC∩BD=F.且△PAD与△ABD均为正三角形,E为AD的中点,G为△PAD重心. 已知如图:三棱柱ABC-A1B1C1的各条棱均相等,AA1⊥平面ABC,E为AA1的中点.
已知如图:三棱柱ABC-A1B1C1的各条棱均相等,AA1⊥平面ABC,E为AA1的中点.