Question

给出下列命题：
①在△ABC中，若A＜B，则sinA＜sinB；
②在同一坐标系中，函数y=sinx与y=lgx的交点个数为2个；
③将函数y=sin（2x+

π

3

）的图象向右平移

π

3

个单位长度可得到函数y=sin2x的图象；
④存在实数x，使得等式sinx+cosx=

3

2

成立；
其中正确的命题为

 

（写出所有正确命题的序号）．

Answer 1

考点：命题的真假判断与应用

专题：阅读型,函数的性质及应用,三角函数的图像与性质

分析：①运用三角形的边角关系和正弦定理，即可判断；
②在同一坐标系中，分别作出函数y=sinx与y=lgx的图象，由图象观察即可得到；
③将函数y=sin（2x+

π

3

）的图象向右平移

π

3

个单位长度，是针对x而言，x-

π

3

代入即可；
④由于sinx+cosx=

2

sin（x+

π

4

）≤

2

，而

3

2

＞

2

，即可判断．

解答： 解：①在△ABC中，若A＜B，则a＜b，即2RsinA＜2RsinB，则sinA＜sinB，故①对；
②在同一坐标系中，分别作出函数y=sinx与y=lgx的图象，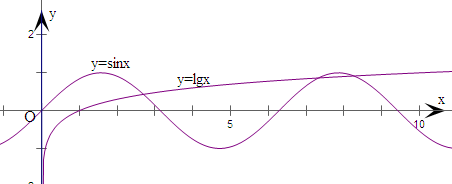
由图象得有3个交点，故②错；
③将函数y=sin（2x+

π

3

）的图象向右平移

π

3

个单位长度
可得到函数y=sin[2（x-

π

3

）+

π

3

]=sin（2x-

π

3

）的图象，故③错；
④由于sinx+cosx=

2

sin（x+

π

4

）≤

2

，而

3

2

＞

2

，则不存在实数x，
使得等式sinx+cosx=

3

2

成立，故④错．
故答案为：①

点评：本题考查三角函数的图象及变换，注意左右平移，针对自变量x而言，同时考查三角形的正弦定理，属于基础题．