题目内容
若R上的减函数f(x)满足f(
)>f(1),则实数x的取值范围 .
| 1 |
| x |
考点:其他不等式的解法,函数单调性的性质
专题:函数的性质及应用
分析:由已知中函数f(x)为R上的减函数,将不等式f(
)>f(1)化为分式不等式,解不等式即可得到答案.
| 1 |
| x |
解答:
解:∵函数f(x)为R上的减函数,
又∵f(
)>f(1),
∴
<1,
解得1<x或x<0.
故实数x的取值范围是{x|1<x或x<0}
故答案为:{x|1<x或x<0}.
又∵f(
| 1 |
| x |
∴
| 1 |
| x |
解得1<x或x<0.
故实数x的取值范围是{x|1<x或x<0}
故答案为:{x|1<x或x<0}.
点评:本题考查的知识点是函数单调性的性质,分式不等式的解法,其中根据函数的单调性将原不等式化为一元二次不等式是解答本题的关键.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
已知点P(a,b),点A在直线l:3x+4y-12=0上,若y=|3a+4b-12|,则y的值与|AP|的关系为( )
| A、y=|AP| |
| B、y=5|AP| |
| C、y≤5|AP| |
| D、y≥5|AP| |
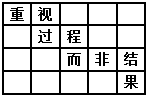 将“重视过程而非结果”8个汉字填入5*4的方格内,其中“重”字填入左上角,“果”字填入右下角,将其余6个汉字依次填入方格,要求只能向右或向下读成一句原话,如图所示为一种填法,则共有
将“重视过程而非结果”8个汉字填入5*4的方格内,其中“重”字填入左上角,“果”字填入右下角,将其余6个汉字依次填入方格,要求只能向右或向下读成一句原话,如图所示为一种填法,则共有