题目内容
9. 如图,四边形ABCD为梯形,AB∥CD,PD⊥平面ABCD,∠BAD=∠ADC=90°,$DC=2AB=2,DA=\sqrt{3}$.
如图,四边形ABCD为梯形,AB∥CD,PD⊥平面ABCD,∠BAD=∠ADC=90°,$DC=2AB=2,DA=\sqrt{3}$.(1)线段BC上是否存在一点E,使平面PBC⊥平面PDE?若存在,请给出$\frac{BE}{CE}$的值,并进行证明;若不存在,请说明理由.
(2)若$PD=\sqrt{3}$,线段PC上有一点F,且PC=3PF,求直线AF与平面PBC所成角的正弦值.
分析 (1)连结DE,PE,BD,便可得到BD=DC,而E又是BC中点,从而得到BC⊥DE,而由PD⊥平面ABCD便可得到BC⊥PD,从而得出BC⊥平面PDE,根据面面垂直的判定定理即可得出平面PBC⊥平面PDE;
(2)建立如图所示的坐标系,求出平面PBC的法向量,即可求直线AF与平面PBC所成角的正弦值.
解答 解: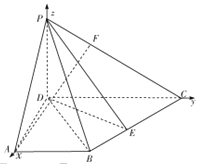 (1)$\frac{BE}{CE}$=1时,平面PBC⊥平面PDE.
(1)$\frac{BE}{CE}$=1时,平面PBC⊥平面PDE.
证明:连结DE,PE,BD,∠BAD=90°,AB=1,DA=$\sqrt{3}$,
∴BD=DC=2a,E为BC中点,∴BC⊥DE;
又PD⊥平面ABCD,BC?平面ABCD;
∴BC⊥PD,DE∩PD=D;
∴BC⊥平面PDE;
∵BC?平面PBC;
∴平面PBC⊥平面PDE;
(2)建立如图所示的坐标系,则D(0,0,0),P(0,0,$\sqrt{3}$),A($\sqrt{3}$,0,0),B($\sqrt{3}$,1,0),C(0,2,0),
∵PC=3PF,∴F(0,$\frac{2}{3}$,$\frac{2\sqrt{3}}{3}$),
∴$\overrightarrow{AF}$=(-$\sqrt{3}$,$\frac{2}{3}$,$\frac{2\sqrt{3}}{3}$),
设平面PBC的法向量为$\overrightarrow{n}$=(x,y,z),
∵$\overrightarrow{BC}$=(-$\sqrt{3}$,1,0),$\overrightarrow{PC}$=(0,2,-$\sqrt{3}$),
∴$\left\{\begin{array}{l}{-\sqrt{3}x+y=0}\\{2y-\sqrt{3}z=0}\end{array}\right.$,取$\overrightarrow{n}$=(1,$\sqrt{3}$,2).
∴直线AF与平面PBC所成角的正弦值=|$\frac{-\sqrt{3}+\frac{2\sqrt{3}}{3}+\frac{4\sqrt{3}}{3}}{\sqrt{8}×\sqrt{\frac{43}{9}}}$|=$\frac{3\sqrt{258}}{172}$.
点评 本题考查线面垂直的性质,线面垂直的判定定理,考查线面角,考查向量知识的运用,属于中档题..

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
| A. | 16+4$\sqrt{5}$ | B. | 20+4$\sqrt{5}$ | C. | 16+8$\sqrt{5}$ | D. | 8+12$\sqrt{5}$ |
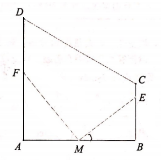 某养殖场原有一块直角梯形的水域ABCD,其中BC,AD与边AB垂直,AD=800m,AB=2BC=600m.为满足钓鱼爱好者需要,计划修建两道互相垂直的水上栈道MF与ME,点M,E,F都在岸边上,其中M为AB的中点,点E在岸边BC上,设∠EMB=θrad,水上栈道MF与ME的长度和记为f(θ)(单位:m).
某养殖场原有一块直角梯形的水域ABCD,其中BC,AD与边AB垂直,AD=800m,AB=2BC=600m.为满足钓鱼爱好者需要,计划修建两道互相垂直的水上栈道MF与ME,点M,E,F都在岸边上,其中M为AB的中点,点E在岸边BC上,设∠EMB=θrad,水上栈道MF与ME的长度和记为f(θ)(单位:m).