题目内容
17.已知等差数列{an}中,a1=3,a2+a5=11.(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)若cn=2${\;}^{{a}_{n}-2}$+n,求数列{cn}的前10项和S10.
分析 (Ⅰ)由已知等式求出公差,然后求通项公式;
(Ⅱ)由(Ⅰ)化简得到数列{cn}的通项公式,利用分组求和得到所求.
解答 解:(Ⅰ)等差数列{an}中,a1=3,a2+a5=11=a1+a6.
所以a6=8,所以公差为1,所以an=n+2;
(Ⅱ)所以cn=2${\;}^{{a}_{n}-2}$+n=2n+n,
所以数列{cn}的前10项和S10=(1+2+…+10)+(2+22+23+…+210)=$\frac{10×11}{2}+\frac{2×(1-{2}^{10})}{1-2}$=55-2+211=53+211.
点评 本题考查了等差数列的通项公式以及对数列分组求和;属于常规题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.若直线3x-4y+5=0与圆x2+y2=r2(r>0)相交于A,B两点且∠AOB=120°则r=( )
| A. | 1 | B. | 2 | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\sqrt{3}$ |
8.已知函数f(x)=loga(x-$\sqrt{2}$+1)+2$\sqrt{2}$(a>0,a≠1)的图象经过定点P,且点P在幂函数g(x)的图象上,则g(x)的表达式为( )
| A. | g(x)=x2 | B. | $g(x)=\frac{1}{x}$ | C. | g(x)=x3 | D. | $g(x)={x^{\frac{1}{2}}}$ |
12.过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左焦点F作直线l与双曲线交于A,B两点,使得|AB|=4b,若这样的直线有且仅有两条,则离心率e的取值范围是( )
| A. | $({1,\frac{{\sqrt{5}}}{2}})$ | B. | $({\sqrt{5},+∞})$ | C. | $({\frac{{\sqrt{5}}}{2},\sqrt{5}})$ | D. | $({1,\frac{{\sqrt{5}}}{2}})∪({\sqrt{5},+∞})$ |
6.命题“?x0∈R,$x_0^2+{x_0}+1<0$”的否定是( )
| A. | 不存在x0∈R,$x_0^2+{x_0}+1≥0$ | B. | ?x0∈R,$x_0^2+{x_0}+1≥0$ | ||
| C. | ?x∈R,x2+x+1<0 | D. | ?x∈R,x2+x+1≥0 |
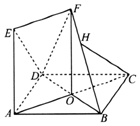 如图,正方形ABCD的对角线AC与BD相交于点O,四边形OAEF为矩形,平面OAEF⊥平面ABCD,AB=AE.
如图,正方形ABCD的对角线AC与BD相交于点O,四边形OAEF为矩形,平面OAEF⊥平面ABCD,AB=AE.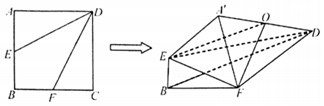
 如图,四边形ABCD为梯形,AB∥CD,PD⊥平面ABCD,∠BAD=∠ADC=90°,$DC=2AB=2,DA=\sqrt{3}$.
如图,四边形ABCD为梯形,AB∥CD,PD⊥平面ABCD,∠BAD=∠ADC=90°,$DC=2AB=2,DA=\sqrt{3}$.