题目内容
已知α,β,γ是不同的平面,m,n是不同的直线,给出下列4个命题:
①若α⊥γ,β⊥γ,则α∥β;
②若α⊥β,β⊥γ,则α⊥γ;
③若m⊥α,α⊥β,则m∥β;
④若m⊥α,n⊥α,则m∥n.
则其中真命题的个数为 个.
①若α⊥γ,β⊥γ,则α∥β;
②若α⊥β,β⊥γ,则α⊥γ;
③若m⊥α,α⊥β,则m∥β;
④若m⊥α,n⊥α,则m∥n.
则其中真命题的个数为
考点:空间中直线与平面之间的位置关系
专题:空间位置关系与距离
分析:利用面面垂直以及线面垂直的性质定理和判定定理对四个命题分别分析解答.
解答:
解:对于①,若α⊥γ,β⊥γ,则α,β的有可能相交,故①错误;
对于②,若α⊥β,β⊥γ,则α,γ有可能平行,故②错误;
对于③,若m⊥α,α⊥β,则m∥β或者m?β;故③错误;
对于④,若m⊥α,n⊥α,则m∥n正确;
故答案为:1.
对于②,若α⊥β,β⊥γ,则α,γ有可能平行,故②错误;
对于③,若m⊥α,α⊥β,则m∥β或者m?β;故③错误;
对于④,若m⊥α,n⊥α,则m∥n正确;
故答案为:1.
点评:本题考查了面面垂直以及线面垂直的性质定理和判定定理的运用,关键是熟练运用定理,明确定理的题设和结论.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
已知椭圆
+
=1(a1>b1>0)的离心率为
,双曲线
-
=1(a2>0,b2>0)与椭圆有相同的焦点F1,F2,M是两曲线的一个公共点,若∠F1MF2=60°,则双曲线的渐进线方程为( )
| x2 | ||
|
| y2 | ||
|
| ||
| 2 |
| x2 | ||
|
| y2 | ||
|
A、y=±
| ||||
| B、y=±x | ||||
C、y=±
| ||||
D、y=±
|
满足tanA>-1的三角形内角A的取值范围是( )
A、(0,
| ||||||
B、(0,
| ||||||
C、(
| ||||||
D、(0,
|
一个侧棱与底面垂直的四棱柱的正视图和俯视图如图所示,该四棱柱的体积为( )


A、
| ||||
B、
| ||||
C、
| ||||
D、
|
一个几何体的三视图如图所示,其中正视图是一个正三角形,则该几何体的体积为( ) 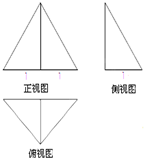

| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
偶函数f(x)的图象如图所示,则f(-1),f(-
),f(
)的大小关系是( )
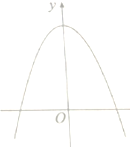
| 2 |
| 3 |

A、f(-1)<f(-
| ||||
B、f(
| ||||
C、f(-
| ||||
D、f(-1),f(
|
 在“2013唱响资阳”电视歌手大赛中,七位评委给甲、乙两名选手打出的分数的茎叶图如右图所示,则甲、乙两名选手得分的中位数之和为
在“2013唱响资阳”电视歌手大赛中,七位评委给甲、乙两名选手打出的分数的茎叶图如右图所示,则甲、乙两名选手得分的中位数之和为