题目内容
16.定义在R上的奇函数f(x)满足f(x+2)=-$\frac{1}{f(x)}$,且在(0,1)上f(x)=3x,则f(log354)=( )| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | -$\frac{3}{2}$ | D. | -$\frac{2}{3}$ |
分析 由条件和函数周期性的定义求出函数的周期,利用函数的周期性、奇函数的性质和函数的解析式,逐步转化由运算性质求出f(log354)的值.
解答 解:由f(x+2)=-$\frac{1}{f(x)}$得,f(x+4)=-$\frac{1}{f(x+2)}$=f(x),
所以函数f(x)的周期是4,
因为f(x)定义在R上的奇函数,且3<log354<4,
且在(0,1)上f(x)=3x,
所以f(log354)=f(log354-4)=-f(4-log354)
=-(${3}^{4-lo{g}_{3}^{54}}$)=-$\frac{81}{54}$=-$\frac{3}{2}$,
故选:C.
点评 本题考查函数值的求法,对数函数的性质、运算性质,及函数的周期性、奇函数的性质的综合应用,利用条件求出函数的周期、以及利用函数的性质逐步转化自变量是解题的关键.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
7.已知集合M={x∈N|x2-5x-6<0},N={x∈Z|2<x<23},则M∩N=( )
| A. | (2,6) | B. | {3,4,5} | C. | {2,3,4,5,6} | D. | [2,6] |
8.已知函数f(x)=$\left\{\begin{array}{l}{ln(x+1),x≥0}\\{-x{e}^{x},x<0}\end{array}\right.$,方程f2(x)+mf(x)=0(m∈R)有四个不相等的实数根,则实数m的取值范围是( )
| A. | (-∞,-$\frac{1}{e}$) | B. | (-$\frac{1}{e}$,0) | C. | (-$\frac{1}{e}$,+∞) | D. | (0,$\frac{1}{e}$) |
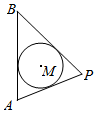 某建筑工地在施工过程中,为了保护一口直径为1米的圆形古井M,决定将其围起来,工地上现有一块长为2米(宽为1.2米)的木工板AB可利用,现将其围成高1.2米的围挡,如图,圆M与AB,PA,PB(PA,PB为另外两侧的围挡)均相切.
某建筑工地在施工过程中,为了保护一口直径为1米的圆形古井M,决定将其围起来,工地上现有一块长为2米(宽为1.2米)的木工板AB可利用,现将其围成高1.2米的围挡,如图,圆M与AB,PA,PB(PA,PB为另外两侧的围挡)均相切.