题目内容
8.已知函数f(x)=$\left\{\begin{array}{l}{ln(x+1),x≥0}\\{-x{e}^{x},x<0}\end{array}\right.$,方程f2(x)+mf(x)=0(m∈R)有四个不相等的实数根,则实数m的取值范围是( )| A. | (-∞,-$\frac{1}{e}$) | B. | (-$\frac{1}{e}$,0) | C. | (-$\frac{1}{e}$,+∞) | D. | (0,$\frac{1}{e}$) |
分析 求出当x<0时,函数f(x)的导数,判断函数的极值,作出函数f(x)的图象,判断函数f(x)=t的根的情况,利用数形结合进行求解即可.
解答 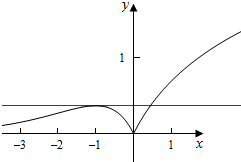 解:当x<0时,f(x)=-xex,
解:当x<0时,f(x)=-xex,
则f′(x)=-(x+1)ex,
由f′(x)=0得x=-1,
当x<-1时,f′(x)>0,
当-1<x<0时,f′(x)<0,
即当x=-1时,函数f(x)取得极大值,此时f(-1)=$\frac{1}{e}$,
且当x<0时,f(x)>0,
当x≥0时,f(x)=ln(x+1)≥0,
设t=f(x),
则当t=$\frac{1}{e}$时,方程t=f(x)有两个根,
当t>$\frac{1}{e}$或t=0时,方程t=f(x)有1个根,
当0<t<$\frac{1}{e}$时,方程t=f(x)有3个根,
当t<0时,方程t=f(x)有0个根,
则方程f2(x)+mf(x)=0(m∈R)等价为t2+mt=0,
即t=0或t=-m,
当t=0时,方程t=f(x)有1个根,
∴若方程f2(x)+mf(x)=0(m∈R)有四个不相等的实数根,
则等价为t=f(x)有3个根,
即0<-m<$\frac{1}{e}$,得-$\frac{1}{e}$<m<0,
故选:B.
点评 本题主要考查函数根的个数的判断,求函数的导数,研究函数的取值范围,利用换元法和图象法进行求解是解决本题的关键.

练习册系列答案
相关题目
19.已知向量$\overrightarrow a=(-1,1)$,|$\overrightarrow b|=(\overrightarrow a+\overrightarrow b)•(\overrightarrow a-3\overrightarrow b)=1$,则<$\overrightarrow a,\overrightarrow b>$等于( )
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{3π}{4}$ |
16.定义在R上的奇函数f(x)满足f(x+2)=-$\frac{1}{f(x)}$,且在(0,1)上f(x)=3x,则f(log354)=( )
| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | -$\frac{3}{2}$ | D. | -$\frac{2}{3}$ |
3.若A,B,C为圆O:x2+y2=1上的三点,且AB=1,BC=2,则$\overrightarrow{BO}$•$\overrightarrow{AC}$=( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{3}{2}$ |
17.设i是虚数单位,若复数$a+\frac{5i}{1-2i}({a∈R})$是纯虚数,则a=( )
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |