题目内容
19.已知函数f(x)=4cosxsin(x+$\frac{π}{6}$)+m(m∈R),当x∈[0,$\frac{π}{2}$]时,f(x)的最小值为-1.(Ⅰ)求m的值;
(Ⅱ)在△ABC中,已知f(C)=1,AC=4,延长AB至D,使BC=BD,且AD=5,求△ACD的面积.
分析 (Ⅰ)利用三角函数恒等变换的应用化简函数解析式可得f(x)=2sin(2x+$\frac{π}{6}$)+m+1.由x∈[0,$\frac{π}{2}$],利用正弦函数的性质可求2sin(2x+$\frac{π}{6}$)min=-1,结合已知可求m的值.
(Ⅱ)由(Ⅰ)可得2sin(2C+$\frac{π}{6}$)=1,结合范围C∈(0,π),可求C=$\frac{π}{3}$,设BD=BC=x,则AB=5-x,在△ACB中,由余弦定理可解得x,进而由余弦定理可求cosA,利用同角三角函数基本关系式可求sinA,利用三角形面积公式即可计算得解.
解答 解:(Ⅰ)∵f(x)=4cosxsin(x+$\frac{π}{6}$)+m
=4cosx(sinxcos$\frac{π}{6}$+cosxsin$\frac{π}{6}$)+m
=$\sqrt{3}$sin2x+2cos2x+m
=$\sqrt{3}$sin2x+cos2x+1+m
=2sin(2x+$\frac{π}{6}$)+m+1.
∵x∈[0,$\frac{π}{2}$],2x+$\frac{π}{6}$∈[$\frac{π}{6}$,$\frac{7π}{6}$],可得:2sin(2x+$\frac{π}{6}$)min=-1,
∴f(x)=-1=-1+m+1,解得:m=-1.
(Ⅱ)∵由(Ⅰ)可得:f(x)=2sin(2x+$\frac{π}{6}$),
∴2sin(2C+$\frac{π}{6}$)=1,
∵C∈(0,π),可得:2C+$\frac{π}{6}$∈($\frac{π}{6}$,$\frac{13π}{6}$),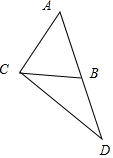
∴2C+$\frac{π}{6}$=$\frac{5π}{6}$,解得:C=$\frac{π}{3}$,
如图,设BD=BC=x,则AB=5-x,
∵在△ACB中,由余弦定理可得:cosC=$\frac{1}{2}$=$\frac{{4}^{2}+{x}^{2}-(5-x)^{2}}{2×4×x}$,解得x=$\frac{3}{2}$,
∴cosA=$\frac{{4}^{2}+(5-\frac{3}{2})^{2}-(\frac{3}{2})^{2}}{2×4×(5-\frac{3}{2})}$=$\frac{13}{14}$,可得:sinA=$\sqrt{1-co{s}^{2}A}$=$\frac{3\sqrt{3}}{14}$,
∴S△ACD=$\frac{1}{2}$AC•AD•sinA=$\frac{1}{2}×5×4×$$\frac{3\sqrt{3}}{14}$=$\frac{15\sqrt{3}}{7}$.
点评 本题主要考查了三角函数恒等变换的应用,正弦函数的性质,余弦定理,同角三角函数基本关系式,三角形面积公式在解三角形中的应用,考查了计算能力和转化思想,属于中档题.

 考前必练系列答案
考前必练系列答案| A. | $\frac{2014}{2015}$ | B. | $\frac{2015}{2016}$ | C. | $\frac{2016}{2017}$ | D. | $\frac{2017}{2018}$ |
| A. | $({-\frac{1}{2},\frac{1}{3}})$ | B. | (-1,2) | C. | $({-\frac{4}{3},-\frac{1}{2}})$ | D. | (-2,3) |

| A. | 7 | B. | 6 | C. | 5 | D. | 3 |
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{7}$ |
| A. | $μ=\sqrt{3},Dξ=\sqrt{7}$ | B. | $μ=\sqrt{3},Dξ=7$ | C. | μ=3,Dξ=7 | D. | $μ=3,Dξ=\sqrt{7}$ |
 如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,且△ABC为等边三角形,AA1=AB=6,D为AC的中点.
如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,且△ABC为等边三角形,AA1=AB=6,D为AC的中点.