题目内容
16．有6人入住某家庭旅馆的6个不同房间，其中的一楼有两个房间，二楼有两个房间，三楼有两个房间，若每人随机地入住这6个房间中的一个房间，则其中的甲乙两人恰好在同一楼层的两个房间的概率为（ ）| A． | $\frac{5}{12}$ | B． | $\frac{1}{5}$ | C． | $\frac{3}{8}$ | D． | $\frac{11}{24}$ |
分析 只考虑甲乙两人，可得总的方法种数为${A}_{6}^{2}$，满足题意的3${A}_{2}^{2}$，由古典概型概率公式可得．
解答 解：只考虑甲乙两人，总的方法种数为${A}_{6}^{2}$=30种，
而甲乙两人恰好在同一楼层的两个房间共有3${A}_{2}^{2}$=6种，
故所求概率P=$\frac{6}{30}$=$\frac{1}{5}$
故选：B
点评 本题考查古典概型及其概率公式，属基础题．
练习册系列答案
相关题目
7．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）两条渐近线的夹角为60°，则该双曲线的离心率为（ ）
| A． | $\frac{{2\sqrt{3}}}{3}$ | B． | $\frac{4}{3}$ | C． | $\frac{{2\sqrt{3}}}{3}$或2 | D． | 4 |
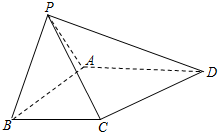如图，在四棱锥P-ABCD中，锐角三角形PAB所在的平面与底面ABCD垂直，∠PBC=∠BAD=90°．
5．已知集合M={x|2x≥1，x∈R}，集合N={x||x-2|≥3，x∈R}，则M∩N=（ ）
| A． | （-∞，-1] | B． | [-1，0] | C． | [5，+∞） | D． | ∅ |