题目内容
已知函数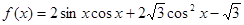 ,
,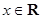 .
.
(1)求函数 的最小正周期和单调递减区间;
的最小正周期和单调递减区间;
(2)已知 中的三个内角
中的三个内角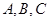 所对的边分别为
所对的边分别为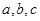 ,若锐角
,若锐角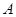 满足
满足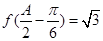 ,且
,且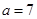 ,
,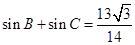 ,求
,求 的面积.
的面积.
(1)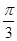 ;
;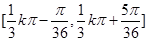 ,
,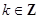 (2)
(2)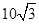
解析试题分析:(1)利用二倍角公式先将 降次,再利用辅助角公式,化成一个角的三角函数,然后求出
降次,再利用辅助角公式,化成一个角的三角函数,然后求出 的解析式
的解析式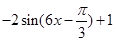 ,利用周期公式求出周期,令
,利用周期公式求出周期,令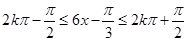 ,解出
,解出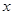 的范围就是
的范围就是 的等单调减区间;(2)由
的等单调减区间;(2)由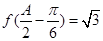 求出sinA,再利用正弦定理及条件
求出sinA,再利用正弦定理及条件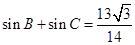 求出b+c,用余弦定理求出bc,再用三角形面积公式求出面积.
求出b+c,用余弦定理求出bc,再用三角形面积公式求出面积.
试题解析:(1)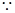
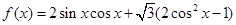
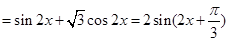
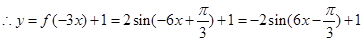
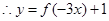 的最小正周期为
的最小正周期为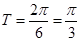 3分
3分
由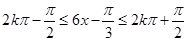 得:
得: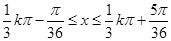 ,
,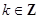 ,
, 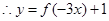 的单调递减区间是
的单调递减区间是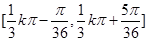 ,
,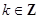 6分
6分
(2)∵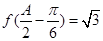 ,∴
,∴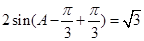 ,∴
,∴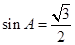 7分
7分
∵ ,∴
,∴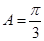 .由正弦定理得:
.由正弦定理得: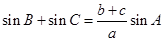 ,
,
即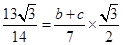 ,∴
,∴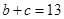 9分
9分
由余弦定理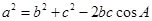 得:
得: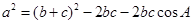 ,
,
即 ,∴
,∴ 11分
11分
∴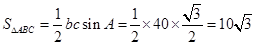 12分
12分
考点:三角恒等变换;三角函数性质;正弦定理;余弦定理;运算求解能力

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
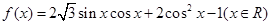 ,
,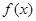 的最小正周期及在区间
的最小正周期及在区间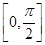 上的最大值和最小值;
上的最大值和最小值;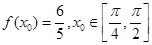 ,求
,求 的值.
的值. .
. ;
; 是第三象限角,且
是第三象限角,且 ,求
,求 的符号称二阶行列式,现规定
的符号称二阶行列式,现规定 , 函数
, 函数 =
= 在一个周期内的图象如图所示,
在一个周期内的图象如图所示, 为图象的最高点,
为图象的最高点,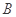 、
、 为图象与
为图象与 轴的交点,且
轴的交点,且 为正三角形。
为正三角形。 的值及函数
的值及函数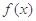 的单调递增区间;
的单调递增区间; ,在
,在 上恒成立,求
上恒成立,求 的取值范围.
的取值范围.
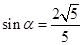 ,
,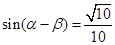 ,且
,且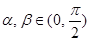 .求:
.求: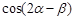 的值;(2)
的值;(2) 的值.
的值. ,
, .
.  ;
;
 的最小正周期;
的最小正周期; 的值.
的值. 的单调增区间
的单调增区间
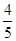 ,求点B(xB,yB)坐标;
,求点B(xB,yB)坐标; =
=