题目内容
3.已知在△ABC中,内角A,B,C所对的边分别为a,b,c,若sinB=2sinA,c>$\sqrt{3}$a.(1)求B的取值范围;
(2)当C=$\frac{2π}{3}$,AB边上的中线长为l时,求S△ABC.
分析 (1)由已知及正弦定理可得:b=2a,利用余弦定理可求cosB>0,结合B∈(0,π),可得B的范围.
(2)由已知及余弦定理可得:c2=a2+b2+ab,又由中线长定理可得c2=2a2+2b2-4,结合已知可求a,b的值,进而利用三角形面积公式即可计算得解.
解答 解:(1)∵sinB=2sinA,c>$\sqrt{3}$a,由正弦定理可得:b=2a,
∴cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$>$\frac{{a}^{2}+3{a}^{2}-4{a}^{2}}{2ac}$=0,
∴结合B∈(0,π),可得:B∈(0,$\frac{π}{2}$).
(2)∵C=$\frac{2π}{3}$,由余弦定理可得:c2=a2+b2+ab,
又∵由中线长定理可得:a2+b2=2[($\frac{c}{2}$)2+12],可得:c2=2a2+2b2-4,
∴2a2+2b2-4=a2+b2+ab,
∵b=2a,
可得:a=$\frac{2\sqrt{3}}{3}$,b=$\frac{4\sqrt{3}}{3}$,
∴S△ABC=$\frac{1}{2}$absinC=$\frac{1}{2}×$$\frac{2\sqrt{3}}{3}$×$\frac{4\sqrt{3}}{3}$×$\frac{\sqrt{3}}{2}$=$\frac{2\sqrt{3}}{3}$.
点评 本题主要考查了正弦定理,余弦定理,中线长定理,三角形面积公式在解三角形中的应用,考查了计算能力和转化思想,属于中档题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
8.小明在花店定了一束鲜花,花店承诺将在第二天旱上7:30~8:30之间将鲜花送到小明家,若小明第二天离开家去公司上班的时间在早上8:00~9:00之间,则小明在离开家之前能收到这束鲜花的概率是( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{7}{8}$ |
15.已知等差数列{an}的前n项和为Sn,a5=10,且S6+3a7=S8+12,则公差d等于( )
| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
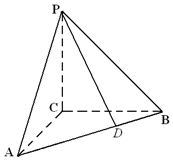 如图,在三棱锥P-ABC中,PC⊥平面ABC,PC=4,AC=BC=3,∠ACB=90°.点D在线段AB上,AD=2DB.
如图,在三棱锥P-ABC中,PC⊥平面ABC,PC=4,AC=BC=3,∠ACB=90°.点D在线段AB上,AD=2DB.