题目内容
12.在△ABC中,内角A,B,C的对边分别为a,b,c,已知2acosB=2c-b,若O是△ABC外接圆的圆心,且$\frac{cosB}{sinC}•\overrightarrow{AB}+\frac{cosC}{sinB}•\overrightarrow{AC}=m\overrightarrow{AO}$,则m=$\sqrt{3}$.分析 由2acosB=2c-b,利用余弦定理求出A=$\frac{π}{3}$;
由O是△ABC外接圆的圆心,取AB中点D,得$\overrightarrow{AO}$=$\overrightarrow{AD}$+$\overrightarrow{DO}$,
化简$\frac{cosB}{sinC}$•$\overrightarrow{AB}$+$\frac{cosC}{sinB}$•$\overrightarrow{AC}$=m$\overrightarrow{AC}$=m($\overrightarrow{AD}$+$\overrightarrow{DO}$);
两边都乘以$\overrightarrow{AB}$,得出$\frac{cosB}{sinC}$•c2+$\frac{cosC}{sinB}$•bccosA=$\frac{1}{2}$mc2;
由正弦定理化简,两边同时除以sinC得cosB+cosAcosC=$\frac{1}{2}$msinC,
利用三角形内角和定理与两角和的余弦公式,即可求出m的值.
解答 解:△ABC中,2acosB=2c-b,
∴2a•$\frac{{a}^{2}{+c}^{2}{-b}^{2}}{2ac}$=2c-b,
∴b2+c2-a2=bc,
∴cosA=$\frac{{b}^{2}{+c}^{2}{-a}^{2}}{2bc}$=$\frac{bc}{2bc}$=$\frac{1}{2}$;
又A∈(0,π),∴A=$\frac{π}{3}$;
由O是△ABC外接圆的圆心,取AB中点D,
则有$\overrightarrow{AO}$=$\overrightarrow{AD}$+$\overrightarrow{DO}$,如图所示;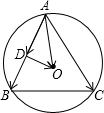
∴$\frac{cosB}{sinC}$•$\overrightarrow{AB}$+$\frac{cosC}{sinB}$•$\overrightarrow{AC}$=m$\overrightarrow{AC}$=m($\overrightarrow{AD}$+$\overrightarrow{DO}$);
由$\overrightarrow{OD}$⊥$\overrightarrow{AB}$得$\overrightarrow{OD}$$•\overrightarrow{AB}$=0,
∴$\frac{cosB}{sinC}$•$\overrightarrow{AB}$•$\overrightarrow{AB}$+$\frac{cosC}{sinB}$•$\overrightarrow{AC}$•$\overrightarrow{AB}$=m($\overrightarrow{AD}$+$\overrightarrow{DO}$)•$\overrightarrow{AB}$
=m$\overrightarrow{AD}$•$\overrightarrow{AB}$+m$\overrightarrow{DO}$•$\overrightarrow{AB}$=$\frac{1}{2}$m${\overrightarrow{AB}}^{2}$,
即$\frac{cosB}{sinC}$•c2+$\frac{cosC}{sinB}$•bccosA=$\frac{1}{2}$mc2;
由正弦定理化简得$\frac{cosB}{sinC}$•sin2C+$\frac{cosC}{sinB}$•sinBsinC•cosA=$\frac{1}{2}$msin2C,
由sinC≠0,两边同时除以sinC得:cosB+cosAcosC=$\frac{1}{2}$msinC,
∴$\frac{1}{2}$m=$\frac{cosB+cosAcosC}{sinC}$
=$\frac{-cos(A+C)+cosAcosC}{sinC}$
=$\frac{-cosAcosC+sinAsinC+cosAcosC}{sinC}$
=sinA=sin$\frac{π}{3}$=$\frac{\sqrt{3}}{2}$,
解得m=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题考查了平面向量,正弦、余弦定理以及两角和的余弦公式,三角形的内角和定理,是综合题题目.

| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | 8 | B. | -a3-3a+4 | C. | 4 | D. | -a3+3a+2 |
| A. | 1+3i | B. | 3-i | C. | $\frac{3}{2}$+$\frac{1}{2}$i | D. | $\frac{1}{2}$+$\frac{3}{2}$i |
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{4}$ | D. | -$\frac{1}{2}$ |