题目内容

已知tanα=
1
3
，tanβ=-
1
7
，且0＜α＜
π
2
，
π
2
＜β＜π，则2α-β的值
 
．
考点：两角和与差的正切函数
专题：三角函数的求值
分析：依题意，可求得tan2α及2α-β的取值范围，利用两角差的正切即可求得tan（2α-β）的值，继而可得2α-β的值．
解答： 解：∵0＜α＜
π
2
，tanα=
1
3
＜1=tan
π
4
，y=tanx在（0，
π
2
）上单调递增，
∴0＜α＜
π
4
，
∴0＜2α＜
π
2
；
又
π
2
＜β＜π，-π＜-β＜-
π
2
；
∴-π＜2α-β＜0，
∵tan2α=
2tanα
1-tan2α
=
2×
1
3
1-(
1
3
)2
=
3
4
，tanβ=-
1
7
，
∴tan（2α-β）=
tan2α-tanβ
1+tan2αtanβ
=
3
4
-(-
1
7
)
1+
3
4
×(-
1
7
)
=1，
∴2α-β=-
3π
4
．
点评：本题考查两角和与差的正切，确定tan2α的值及2α-β的取值范围是关键，也是难点，考查运算求解能力，属于中档题．
练习册系列答案
相关题目
已知函数f（x）=
1
2
ax2-（2a+1）x+2lnx（a＞0）．
（Ⅰ）若a=
1
3
，求f（x）在[1，3]上的最大值；
（Ⅱ）若a≠
1
2
，求函数f（x）的单调区间；
（Ⅲ）当
1
2
＜a＜1时，判断函数f（x）在区间[1，2]上有无零点？写出推理过程．
已知在平面内点P满足|PM|-|PN|=2
2
，M（-2，0），N（ 2，0 ），O（0，0）
（1）求点P的轨迹S；
（2）（理）直线过点（2，0）与S交于点A，B，求△OAB的面积的最小值．
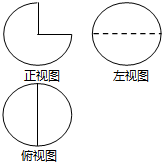一个几何体的三视图如图所示，其中俯视图与左视图均为半径是2的圆，则这个几何体的表面积是
 
．
已知平面向量
a
=（2，3），
b
=（1，m），且
a
∥
b
，则实数m的值为
 
．
已知直线l，m，平面α，β，γ，给出下列命题：
①l∥α，l∥β，α∩β=m，则l∥m  
②α∥β，β∥γ，m⊥α，则m⊥β
③α⊥γ，β⊥γ，则α⊥β  
④l⊥m，l⊥α，m⊥β，则α⊥β
其中正确的命题的序号是
 
．
已知数列{an}中，a1=1，a2n=n-an，a2n+1=an+1，则a1+a2+a3+…+a99=
 
．
（文）已知向量
a
=（-3，-4），
b
=（0，1），点C对应的向量
c
=
a
+λ
b
，且C点在函数y=cos
π
3
x的图象上，则实数λ=
 
．
设（1-
2
x
）4=a0+a1（
1
x
）+a2（
1
x
）2+a3（
1
x
）3+a4（
1
x
）4，则a2+a4的值是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网