题目内容
(文科)方程|x2+2x|=ax+1有且仅有三个实数解,则a= .
考点:根的存在性及根的个数判断,函数的零点与方程根的关系
专题:函数的性质及应用
分析:将方程转化为函数,利用数形结合即可得到结论.
解答:
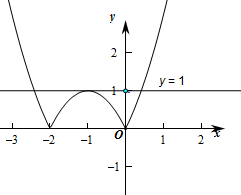 解:设f(x)=|x2+2x|=
解:设f(x)=|x2+2x|=
,
当-2<x<0时,f(x)=-x2-2x=-(x+1)2+1∈(0,1],
作出函数f(x)的图象如图,
由函数y=ax+1过定点(0,1),
要使方程|x2+2x|=ax+1有且仅有三个实数解,
即等价为函数f(x)=|x2+2x|和y=ax+1的图象有且仅有三个交点,
由图象可知a=1,
故答案为:1
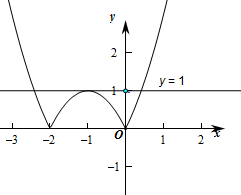 解:设f(x)=|x2+2x|=
解:设f(x)=|x2+2x|=
|
当-2<x<0时,f(x)=-x2-2x=-(x+1)2+1∈(0,1],
作出函数f(x)的图象如图,
由函数y=ax+1过定点(0,1),
要使方程|x2+2x|=ax+1有且仅有三个实数解,
即等价为函数f(x)=|x2+2x|和y=ax+1的图象有且仅有三个交点,
由图象可知a=1,
故答案为:1
点评:本题主要考查方程根的个数的应用,利用方程和函数之间的关系,转化为两个函数图象问题,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
 如图,已知棱长为1的正方体中ABCD-A1B1C1D1中,P,Q是面对角线A1C1上的两个不同动点,给出以下判断:
如图,已知棱长为1的正方体中ABCD-A1B1C1D1中,P,Q是面对角线A1C1上的两个不同动点,给出以下判断: