题目内容
3.定义平面向量之间的一种运算“⊙”如下:对任意的$\overrightarrow a=(m,n),\overrightarrow b=(p,q)$(其中m,n,p,q均为实数),令$\overrightarrow a⊙\overrightarrow b=mq-np$.在下列说法中:(1)若向量$\overrightarrow a与\overrightarrow b$共线,则$\overrightarrow a⊙\overrightarrow b=0$;
(2)$\overrightarrow a⊙\overrightarrow b=\overrightarrow b⊙\overrightarrow a$;
(3)对任意$λ∈R,有(λ\overrightarrow a)⊙\overrightarrow b=λ(\overrightarrow a⊙\overrightarrow b)$;
(4)${(\overrightarrow a⊙\overrightarrow b)^2}+{(\overrightarrow a•\overrightarrow b)^2}={|{\overrightarrow a}|^2}{|{\overrightarrow b}|^2}$(其中$\overrightarrow a•\overrightarrow b$表示$\overrightarrow a与\overrightarrow b$的数量积,$|{\overrightarrow a}$|表示向量的模).
正确的说法是(1),(3),(4).(写出所有正确的说法的序号)
分析 根据新定义,逐项计算式子的两端,验证是否相等.
解答 解:对于(1),若向量$\overrightarrow a与\overrightarrow b$共线,则mq-np=0,∴$\overrightarrow a⊙\overrightarrow b=0$,故(1)正确;
对于(2),$\overrightarrow{b}$⊙$\overrightarrow{a}$=pn-qm,$\overrightarrow a⊙\overrightarrow b=mq-np$,故(2)不正确;
对于(3),($λ\overrightarrow{a}$)⊙$\overrightarrow{b}$=(λm,λn)⊙(p,q)=λmq-λnp,λ($\overrightarrow{a}$⊙$\overrightarrow{b}$)=λ(mq-np)=λmq-λnp.故(3)正确;
对于(4),($\overrightarrow{a}$⊙$\overrightarrow{b}$)2+($\overrightarrow{a}•\overrightarrow{b}$)2=(mq-np)2+(mp+nq)2=m2q2+n2p2+m2p2+n2q2=(m2+n2)(p2+q2),|$\overrightarrow{a}$|2=m2+n2,|$\overrightarrow{b}$|2=p2+q2,故(4)正确.
故答案为:(1),(3),(4).
点评 本题考查了平面向量的数量积运算和新定义运算,根据新定义计算是关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
11.直线l1:3mx+8y+3m-10=0过定点( )
| A. | (-1,-$\frac{4}{5}$) | B. | (-1,$\frac{4}{5}$) | C. | (-1,$\frac{5}{4}$) | D. | (-1,-$\frac{5}{4}$) |
12.如图,在正方体ABCD-A1B1C1D1中,M为棱D1C1的中点.设AM与平面BB1D1D的交点为O,则( )
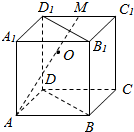

| A. | 三点D1,O,B共线,且OB=2OD1 | B. | 三点D1,O,B不共线,且OB=2OD1 | ||
| C. | 三点D1,O,B共线,且OB=OD1 | D. | 三点D1,O,B不共线,且OB=OD1 |
13.从自然数1,2,3,4,5中,任意取出两个数组成两位的自然数,则在两位自然数中取出的数恰好能被3整除的概率为( )
| A. | $\frac{2}{5}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{10}$ | D. | $\frac{1}{2}$ |