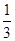题目内容
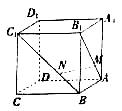
正方体ABCD—A1B1C1D1中直线 与平面
与平面 夹角的余弦值是( )
夹角的余弦值是( )
A. | B. | C. | D. |
C
解析试题分析:以D点为原点,以 所在的直线分别为
所在的直线分别为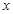 轴,
轴, 轴,
轴, 轴建立空间直角坐标系,
轴建立空间直角坐标系,
设正方体的棱长为1,则 ,平面
,平面 的一个法向量为
的一个法向量为 ,设直线
,设直线 与平面
与平面 夹角为
夹角为 ,则
,则 =
=
 ,所以
,所以 .
.
考点:本题考查的知识点是空间向量在立体几何中的应用,要求熟练掌握利用向量方法来求空间中线面所成角的方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如下图,在正方体ABCD-A1B1C1D1中,P为对角线BD1的三等分点,则P到各顶点距离的不同取值有( )
| A.6个 | B.5个 | C.4个 | D.3个 |
如图,在正方体ABCD﹣A1B1C1D1中,M,N分别是BC1,CD1的中点,则下列说法错误的是( )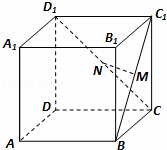
| A.MN与CC1垂直 | B.MN与AC垂直 | C.MN与BD平行 | D.MN与A1B1平行 |
在正方体 中,
中,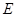 是
是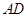 的中点,则异面直线
的中点,则异面直线 与
与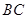 所成的角的余弦值是( )
所成的角的余弦值是( )
A. | B. | C. | D. |
给定下列四个命题:
①若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;
②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;
③垂直于同一直线的两条直线相互平行;
④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.
其中,为真命题的是( )
| A.①和② | B.②和③ | C.③和④ | D.②和④ |
已知三条不重合的直线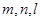 ,两个不重合的平面
,两个不重合的平面 ,有下列命题:
,有下列命题:
①若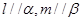 ,且
,且 ,则
,则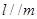
②若 ,且
,且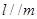 ,则
,则
③若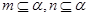 ,
,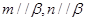 ,则
,则
④若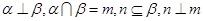 ,则
,则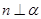
其中真命题的个数是( )
| A.4 | B.3 | C.2 | D.1 |

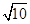
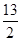
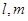 ,平面
,平面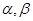 ,且
,且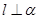 ,
,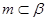 ,给出下列四个命题:
,给出下列四个命题: ∥
∥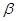 ,则
,则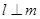 ;
;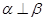 ,则
,则 ∥
∥ ;
;