题目内容
如图,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中
点.将△ADE与△BEC分别沿ED、EC向上折起,使A、B重合于点P,则三棱锥P-DCE的外接球的体积为( )
A. B.
B. C.
C.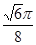 D.
D.
C
解析试题分析:易证所得三棱锥为正四面体,它的棱长为1,
故外接球半径为 ,外接球的体积为
,外接球的体积为 ,故选C.
,故选C.
故选C.
考点:球内接多面体;球的体积和表面积.
点评:本题考查球的内接多面体,球的体积等知识,考查逻辑思维能力,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知圆柱 底面半径为1,高为
底面半径为1,高为 ,
, 是圆柱的一个轴截面.动点
是圆柱的一个轴截面.动点 从点
从点 出发沿着圆柱的侧面到达点
出发沿着圆柱的侧面到达点 ,其距离最短时在侧面留下的曲线
,其距离最短时在侧面留下的曲线 如图所示.
如图所示.
现将轴截面 绕着轴
绕着轴 逆时针旋转
逆时针旋转 后,边
后,边 与曲线
与曲线 相交于点
相交于点 ,设
,设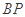 的长度为
的长度为 ,则
,则 的图象大致为( )
的图象大致为( )
某几何体的三视图如图所示,则该几何体的体积不可能是
A. | B. |
C. | D. |
某个几何体的三视图如图所示,其中俯视图为等边三角形,则该几何体的表面积是( )
A. | B. |
C.6+ | D. |
某几何体的三视图如图所示,则其侧面积为( )
A. | B. | C. | D. |




 是边长为
是边长为 的正方形,则该几何体的表面积为
的正方形,则该几何体的表面积为





 ,且一个内角为60°的菱形,俯视图为正方形,那么这个几何体的表面积为
,且一个内角为60°的菱形,俯视图为正方形,那么这个几何体的表面积为


 长为2;侧视图一直角三角形;俯视图为一直角梯形,且
长为2;侧视图一直角三角形;俯视图为一直角梯形,且 ,则此几何体的体积是( )。
,则此几何体的体积是( )。


