题目内容
由两个完全相同的正四棱锥组合而成的空间几何体的正(主)视图、侧(左)视图、俯视图相同,如图所示,其中四边形 是边长为
是边长为 的正方形,则该几何体的表面积为
的正方形,则该几何体的表面积为
A. | B. |
C. | D. |
C
解析试题分析:由三视图可知,构成组合体的两个正四棱锥底面为边长是1的正方形,高为  ,就可求出正四棱锥的侧棱长,又因为空间几何体由两个完全相同的正四棱锥组合而成,且底面重合,所以侧面为8个全等的三角形,只需求出一个三角形的面积,就可得到该几何体的表面积解:由三视图可知,构成组合体的两个正四棱锥底面为边长是1的正方形,高为
,就可求出正四棱锥的侧棱长,又因为空间几何体由两个完全相同的正四棱锥组合而成,且底面重合,所以侧面为8个全等的三角形,只需求出一个三角形的面积,就可得到该几何体的表面积解:由三视图可知,构成组合体的两个正四棱锥底面为边长是1的正方形,高为 ∴正四棱锥的侧楞为1,∴正四棱锥的每一个侧面均为边长是1的正三角形,而组合体的侧面由8个这样的正三角形构成,∴侧面积为,
∴正四棱锥的侧楞为1,∴正四棱锥的每一个侧面均为边长是1的正三角形,而组合体的侧面由8个这样的正三角形构成,∴侧面积为, ×1× 1×
×1× 1× ×8=
×8= 故选C
故选C
考点:组合体表面积
点评:本题考查了组合体表面积的求法,其中给出的图形为三视图,要求学生要具备一定的识图能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在几何体的三视图如图所示,则该几何体的体积为( )
A. | B.2 | C. | D. |
如图是长方体被一平面所截得到的几何体,四边形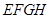 为截面,长方形
为截面,长方形 为底面,则四边形
为底面,则四边形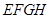 的形状为( )
的形状为( )
| A.梯形 | B.平行四边形 |
| C.可能是梯形也可能是平行四边形 | D.不确定 |
正方体的体积是64,则其表面积是( )
| A.64 | B.16 | C.96 | D.无法确定 |
已知三棱柱

 ( )
( )
A. | B. | C. | D. |


 B.
B. 与
与 相交
相交 D.
D.
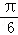 ,则
,则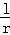 = .
= .

 B.
B. C.
C.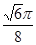 D.
D.