题目内容
某几何体的三视图如图所示,则其侧面积为( )
A. | B. | C. | D. |
A
解析试题分析:从三视图可以推知,几何体是四棱锥,底面是一个直角梯形,一条侧棱垂直底面,易求侧面积解:几何体是四棱锥,底面是一个直角梯形,一条侧棱垂直底面.且底面直角梯形的上底为1,下底为2,高为1,四棱锥的高为1,四个侧面都是直角三角形,其中△PBC的高PB=
故其侧面积是S=S△PAB+S△PBC+S△PCD+S△PAD= ,故可知答案为A.
,故可知答案为A.
考点:三视图求面积
点评:本题考查三视图求面积、体积,考查空间想象能力,是中档题.

练习册系列答案
相关题目
正方体的体积是64,则其表面积是( )
| A.64 | B.16 | C.96 | D.无法确定 |
下列物体的三视图与物体摆放位置无关的是( )
| A.正方体 | B.正四面体 | C.正三棱锥 | D.球 |
某几何体的三视图如图所示,则该几何体的表面积为( )
| A.18 | B.21 | C.24 | D.27 |
长方体一个顶点上三条棱的长分别为3、4、5,且它的八个顶点都在同一球面上,这个球的表面积是( )
A.20 π π | B.25 π π | C.50π | D.200π |
如图是一个几何体的三视图,则该几何体为
| A.球 | B.圆柱 |
| C.圆台 | D.圆锥 |
从一个正方体中截去部分几何体,得到的几何体三视图如下,则此几何体的体积是( )
| A.64 | B. | C. | D. |

 B.
B. C.
C.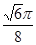 D.
D.
 的棱长为1,动点P在此正方体的表面上运动,且
的棱长为1,动点P在此正方体的表面上运动,且 ,记点P的轨迹的长度为
,记点P的轨迹的长度为 ,则函数的图像
,则函数的图像
