题目内容
如图,一个空间几何体的正视图、侧视图都是面积为
 ,且一个内角为60°的菱形,俯视图为正方形,那么这个几何体的表面积为
,且一个内角为60°的菱形,俯视图为正方形,那么这个几何体的表面积为
A. | B. | C.4 | D.8 |
C
解析试题分析:根据题意,由于一个空间几何体的正视图、侧视图都是面积为
 ,且一个内角为60°的菱形,俯视图为正方形,那么这个几何体为两个正四棱锥的组合体,则其四棱锥的底面边长为1,高为
,且一个内角为60°的菱形,俯视图为正方形,那么这个几何体为两个正四棱锥的组合体,则其四棱锥的底面边长为1,高为 ,四棱锥的组合体,因此其表面积为
,四棱锥的组合体,因此其表面积为 故可知表面积为4,故答案为C
故可知表面积为4,故答案为C
考点:三视图
点评:主要是考查了由三视图来求解棱锥体积的运用,属于中档题。

练习册系列答案
相关题目
在半径为 的球内放入大小相等的4个小球,则小球半径
的球内放入大小相等的4个小球,则小球半径 的最大值为( )
的最大值为( )
A. | B. | C. | D.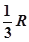 |
一个几何体的三视图如右图所示(单位长度:cm),则此几何体的表面积是( )
| A.16cm2 | B. |
C. | D. |
已知四棱锥 的三视图如图所示,则此四棱锥的四个侧面的面积中最大的是( )
的三视图如图所示,则此四棱锥的四个侧面的面积中最大的是( ) 
| A.2 | B.3 | C. | D. |
某几何体的三视图如图所示,则该几何体的表面积为( )
| A.18 | B.21 | C.24 | D.27 |
 ,直径为4的球的体积为
,直径为4的球的体积为 ,则
,则 ( )
( )





 B.
B. 与
与 相交
相交 D.
D.
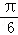 ,则
,则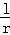 = .
= .

 B.
B. C.
C.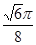 D.
D.