题目内容
4.动点P到两定点F1(0,-4),F2(0,4)的距离之和为10,则动点P的轨迹方程是( )| A. | $\frac{x^2}{16}+\frac{y^2}{9}=1$ | B. | $\frac{x^2}{9}+\frac{y^2}{25}=1$ | C. | $\frac{x^2}{16}+\frac{y^2}{25}=1$ | D. | $\frac{x^2}{100}+\frac{y^2}{36}=1$ |
分析 由题意可知,动点P的轨迹是以F1(0,-4),F2(0,4)为焦点的椭圆,则动点P的轨迹方程可求.
解答 解:动点P到两定点F1(0,-4),F2(0,4)的距离之和为10,
∵10>8=|F1F2|,
∴动点P的轨迹是以F1(0,-4),F2(0,4)为焦点的椭圆,
且a=5,c=4,则b2=a2-c2=25-16=9,
∴动点P的轨迹方程是$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{25}=1$.
故选:B.
点评 本题考查轨迹方程,考查了椭圆的定义,是基础题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
15.下列结论错误的是( )
| A. | 命题“若p,则¬q”与命题“若q,则¬p”互为逆否命题 | |
| B. | 命题p:?x∈[0,1],ex≥1,命题q:?x∈R,x2+x+1<0,则p∧q为真 | |
| C. | “若am2<bm2,则a<b”为真命题 | |
| D. | 若p∨q为假命题,则p、q均为假命题 |
14.如图,长方体ABCD-A1B1C1D1中,AA1=2AB=2AD,则异面直线A1B与AD1所成角的余弦值为( )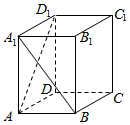

| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |