题目内容
已知函数f（x）=x3+bx2-3x+1（b∈R），在x=x1和x=x2（x1＞x2）处都取得极值，则下列说法正确的是（ ）
| A、f（x）在x=x1处取得极小值，在x=x2处取得极小值 |
| B、f（x）在x=x1处取得极小值，在x=x2处取得极大值 |
| C、f（x）在x=x1处取得极大值，在x=x2处取得极小值 |
| D、f（x）在x=x1处取得极大值，在x=x2处取得极大值 |
考点：利用导数研究函数的极值
专题：导数的综合应用
分析：求出f（x）的导函数，因为函数在x1，x2时取得极值，x=x1和x=x2是导函数等于0的两个根，由此可得f（x）在x=x1处取得极大值，在x=x2处取得极小值．
解答：
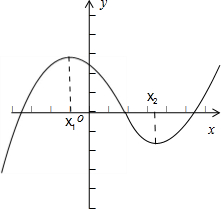解：由于函数f（x）=x3+bx2-3x+1（b∈R），
则f′（x）=3x2+2bx-3（b∈R）
由于函数在x=x1和x=x2（x1＜x2）处都取得极值，
令f′（x）＞0，解得x＜x1或x＞x2；
令f′（x）＜0，解得x1＜x＜x2；
故f（x）在x=x1处取得极大值，在x=x2处取得极小值．
故选：C．
解：由于函数f（x）=x3+bx2-3x+1（b∈R），则f′（x）=3x2+2bx-3（b∈R）
由于函数在x=x1和x=x2（x1＜x2）处都取得极值，
令f′（x）＞0，解得x＜x1或x＞x2；
令f′（x）＜0，解得x1＜x＜x2；
故f（x）在x=x1处取得极大值，在x=x2处取得极小值．
故选：C．
点评：考查学生利用导数求函数极值的能力，利用导数研究函数单调性的能力，以及掌握函数在某点取得极值的条件．
练习册系列答案
课时训练江苏人民出版社系列答案
黄冈经典趣味课堂系列答案
启东小题作业本系列答案
相关题目
已知函数f（x）=-x3，则下列说话正确的是（ ）
| A、f（x）为奇函数，且在（0，+∞）上是增函数 |
| B、f（x）为奇函数，且在（0，+∞）上是减函数 |
| C、f（x）为偶函数，且在（0，+∞）上是增函数 |
| D、f（x）为偶函数，且在（0，+∞）上是偶函数 |
已知集合A={1，2，3，4，5，6}，在A中任取三个元素，使它们的和小于余下的三个元素的和，则取法种数共有（ ）
| A、4 | B、10 | C、15 | D、20 |
设a，b表示直线，α，β，γ表示不同的平面，则下列命题中正确的是（ ）
| A、若a⊥α且a⊥b，则b∥α |
| B、若γ⊥α且γ⊥β，则α∥β |
| C、若a∥α且a∥β，则α∥β |
| D、若γ∥α且γ∥β，则α∥β |