题目内容
某地区的一种特色水果上市时间仅能持续5个月,预测上市初期和后期会因供不应求使价格呈连续上涨态势,而中期又将出现供大于求使价格下跌.经市场分析,价格模拟函数为以下三个函数中的一个:①f(x)=p•qx;②f(x)=px2+qx+1;③f(x)=x(x-q)2+p.(以上三式中p,q均为常数,且q>1)(注:函数的定义域是[0,5]).其中x=0表示4月1日,x=1表示5月1日,…,依此类推.
(Ⅰ)请判断以上哪个价格模拟函数能准确模拟价格变化走势,为什么?
(Ⅱ)若该果品4月1日投入市场的初始价格定为6元,且接下来的一个月价格持续上涨,并在5 月1日达到了一个最高峰,求出所选函数f(x)的解析式;
(Ⅲ)在(Ⅱ)的条件下,为保护果农的收益,打算在价格下跌期间积极拓宽境外销售,且销售价格为该果品上市期间最低价格的2倍,请你预测该果品在哪几个月内价格下跌及境外销售的价格.
(Ⅰ)请判断以上哪个价格模拟函数能准确模拟价格变化走势,为什么?
(Ⅱ)若该果品4月1日投入市场的初始价格定为6元,且接下来的一个月价格持续上涨,并在5 月1日达到了一个最高峰,求出所选函数f(x)的解析式;
(Ⅲ)在(Ⅱ)的条件下,为保护果农的收益,打算在价格下跌期间积极拓宽境外销售,且销售价格为该果品上市期间最低价格的2倍,请你预测该果品在哪几个月内价格下跌及境外销售的价格.
考点:导数在最大值、最小值问题中的应用
专题:应用题
分析:(Ⅰ)从研究三个函数的单调性出发,对照着题目中所说的“上市初期和后期会因供不应求使价格呈连续上涨态势,而中期又将出现供大于求使价格下跌”的市场行情,确定满足题意的函数;
(Ⅱ)由题目中的叙述可知,f(0)=6,f′(1)=0,从中解出两个参数p,q,再写出f(x)的解析式.
(Ⅲ)对f(x)求导,计算其在0≤x≤5时的减区间和最小值,从而确定该果品在哪几个月内价格下跌及境外销售的价格.
(Ⅱ)由题目中的叙述可知,f(0)=6,f′(1)=0,从中解出两个参数p,q,再写出f(x)的解析式.
(Ⅲ)对f(x)求导,计算其在0≤x≤5时的减区间和最小值,从而确定该果品在哪几个月内价格下跌及境外销售的价格.
解答:
解:(Ⅰ)应选f(x)=x(x-q)2+p.
因为①f(x)=p•qx中单调函数;②f(x)=px2+qx+1的图象不具有先升再降后升特征;③f(x)=x(x-q)2+p中,f'(x)=3x2-4qx+q2,令f'(x)=0,得x=q,x=
,f'(x)有两个零点.出现两个递增区间和一个递减区间,符合价格走势;
(Ⅱ)由f(0)=6,f′(1)=0,得
,解得
(q=1舍去).
∴f(x)=x(x-3)2+6,即f(x)=x3-6x2+9x+6(0≤x≤5);
(Ⅲ)由f'(x)<0,解得1<x<3,
所以函数f(x)=x3-6x2+9x+6在区间(1,3)上单调递减,
故这种水果在5月,6月份价格下跌.且境外销售的价格为2×6=12(元)
因为①f(x)=p•qx中单调函数;②f(x)=px2+qx+1的图象不具有先升再降后升特征;③f(x)=x(x-q)2+p中,f'(x)=3x2-4qx+q2,令f'(x)=0,得x=q,x=
| q |
| 3 |
(Ⅱ)由f(0)=6,f′(1)=0,得
|
|
∴f(x)=x(x-3)2+6,即f(x)=x3-6x2+9x+6(0≤x≤5);
(Ⅲ)由f'(x)<0,解得1<x<3,
| x | 0 | (0,1) | 1 | (1,3) | 3 | (3,5) | 5 |
| f(x) | 6 | ↑ | 极大值 10 |
↓ | 极小值 6 |
↑ | 26 |
故这种水果在5月,6月份价格下跌.且境外销售的价格为2×6=12(元)
点评:本题属于较为基础的应用题,题目中所涉及到的数学知识并不复杂,都是基本知识和方法的考查,关键是怎样把现实中的问题抽象成数学问题,这对于学生是一个难点,同时这也是解决大多数应用题的关键所在.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
一个均匀小正方体的六个面中,三个面上标以数0,两个面上标以数1,一个面上标以数3,将这个小正方体抛掷两次,则向上的数之积的数学期望是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
如图所给的程序运行结果为S=35,那么判断框中应填入的关于k的条件是( )


| A、k=7 | B、k≤6 |
| C、k<6 | D、k>6 |

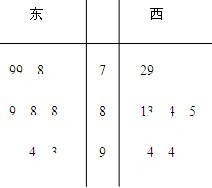 某城市要建成宜商、宜居的国际化新城,该城市的东城区、西城区分别引进8个厂家,现对两个区域的16个厂家进行评估,综合得分情况如茎叶图所示.
某城市要建成宜商、宜居的国际化新城,该城市的东城区、西城区分别引进8个厂家,现对两个区域的16个厂家进行评估,综合得分情况如茎叶图所示.