题目内容
14.已知边长为2的正方形ABCD的四个顶点在球O的球面上,球O的体积为V球=$\frac{160\sqrt{5}π}{3}$,则OA与平面ABCD所成的角的余弦值为( )| A. | $\frac{\sqrt{10}}{10}$ | B. | $\frac{\sqrt{10}}{5}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{2\sqrt{5}}{5}$ |
分析 过球心O作平面ABCD的垂线OG,则G为正方形中心,∠OAG为OA与平面ABCD所成的角,求出球的半径OA,再求出AG,即可得出所求角的余弦值.
解答 解:如图,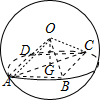
设球O的半径为R,由V球=$\frac{4}{3}π{R}^{3}$=$\frac{160\sqrt{5}π}{3}$,
得${R}^{3}=\sqrt{8000}$,∴R=$2\sqrt{5}$,即OA=$2\sqrt{5}$.
设正方形ABCD的中心为G,连接OG,则OG⊥平面ABCD,
且AG=$\frac{1}{2}AC=\frac{1}{2}×2\sqrt{2}=\sqrt{2}$.
∴OA与平面ABCD所成的角的余弦值为$\frac{AG}{OA}=\frac{\sqrt{2}}{2\sqrt{5}}=\frac{\sqrt{10}}{10}$.
故选:A.
点评 本题考查了线面角的计算,球的结构特征,属于基础题.

练习册系列答案
相关题目
4.${∫}_{0}^{π}$cos$\frac{x}{2}$dx的值是( )
| A. | 2 | B. | 1 | C. | 4 | D. | 5 |
5.已知集合A={y|y=|x|,x∈R},B={y|y2-y-2≤0},则A∩B=( )
| A. | [0,2] | B. | [1,2] | C. | [-1,2] | D. | [-1,0] |
9.设集合M={x|4≤2x≤16},N={x|x(x-3)<0},则M∩N=( )
| A. | (0,3) | B. | [2,3] | C. | [2,3) | D. | (3,4) |
6.用数学归纳法证明不等式1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{{2}^{n}-1}$<n(n∈N*)过程中,由n=k递推到n=k+1时,不等式左端增加的项数是( )
| A. | 1 | B. | 2k-1 | C. | 2k | D. | 2k+1 |
4.在△ABC中,角A、B、C的对边分别为a,b,c,则“a=2bcosC”是“△ABC是等腰三角形”的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |