题目内容
直角三角形ABC的顶点坐标A(-2,0),直角顶点B(0,-2
),顶点C在x轴上
(Ⅰ)求BC边所在直线方程;
(Ⅱ)M为直角三角形ABC外接圆的圆心,求圆M的方程.
| 2 |
(Ⅰ)求BC边所在直线方程;
(Ⅱ)M为直角三角形ABC外接圆的圆心,求圆M的方程.
考点:直线和圆的方程的应用
专题:计算题,直线与圆
分析:(Ⅰ)求出AB的斜率,即可求BC边所在直线方程;
(Ⅱ)直角三角形ABC,圆心为斜边的中点,半径为斜边的一半,可求圆M的方程.
(Ⅱ)直角三角形ABC,圆心为斜边的中点,半径为斜边的一半,可求圆M的方程.
解答:
解:(Ⅰ)∵A(-2,0),B(0,-2
),
∴kAB=-
,kBC=
,
∴BC边所在直线方程:x-
y-4=0-------------------------------(7分)
(Ⅱ)∵直角三角形ABC,圆心为斜边的中点,半径为斜边的一半.
∴圆M的方程:(x-1)2+y2=9-------------------------------(7分)
| 2 |
∴kAB=-
| 2 |
| ||
| 2 |
∴BC边所在直线方程:x-
| 2 |
(Ⅱ)∵直角三角形ABC,圆心为斜边的中点,半径为斜边的一半.
∴圆M的方程:(x-1)2+y2=9-------------------------------(7分)
点评:本题考查直线与圆的方程,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
正三棱锥S-ABC中,若侧棱 SA=4
,高SO=4,则此正三棱锥S-ABC外接球的表面积是( )
| 3 |
| A、36π | B、64π |
| C、144π | D、256π |
半径为R的球,其内接正方体的表面积为( )
| A、4R2 |
| B、6R2 |
| C、8R2 |
| D、10R2 |
 如图所示,AC=BC=1,∠ACB=90°,PA⊥平面ABC,CE∥PA,PA=2CE=2.
如图所示,AC=BC=1,∠ACB=90°,PA⊥平面ABC,CE∥PA,PA=2CE=2.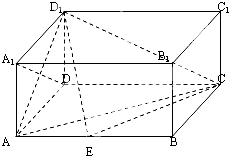 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上.