题目内容
设向量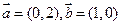 ,过定点
,过定点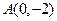 ,以
,以 方向向量的直线与经过点
方向向量的直线与经过点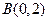 ,以向量
,以向量 为方向向量的直线相交于点P,其中
为方向向量的直线相交于点P,其中
(1)求点P的轨迹C的方程;
(2)设过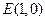 的直线
的直线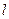 与C交于两个不同点M、N,求
与C交于两个不同点M、N,求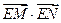 的取值范围
的取值范围
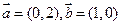 ,过定点
,过定点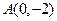 ,以
,以 方向向量的直线与经过点
方向向量的直线与经过点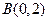 ,以向量
,以向量 为方向向量的直线相交于点P,其中
为方向向量的直线相交于点P,其中
(1)求点P的轨迹C的方程;
(2)设过
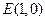 的直线
的直线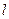 与C交于两个不同点M、N,求
与C交于两个不同点M、N,求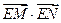 的取值范围
的取值范围(1)点P的轨迹C的方程为
(2)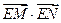 的取值范围是
的取值范围是

(2)
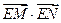 的取值范围是
的取值范围是
(1)设
 ∵
∵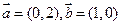 ,
,∴
 ,
, 2分
2分过定点
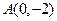 ,以
,以 方向向量的直线方程为:
方向向量的直线方程为:
过定点
 ,以
,以 方向向量的直线方程为:
方向向量的直线方程为:
联立消去
 得:
得: ∴求点P的轨迹C的方程为
∴求点P的轨迹C的方程为 6分
6分(2)当过
 的直线
的直线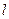 与
与 轴垂直时,
轴垂直时,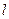 与曲线
与曲线 无交点,不合题意,
无交点,不合题意,∴设直线
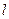 的方程为:
的方程为: ,
,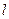 与曲线
与曲线 交于
交于
由



∴


 ∵
∵ ,∴
,∴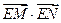 的取值范围是
的取值范围是

练习册系列答案
相关题目
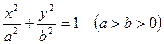 的离心率为,且其焦点F(c,0)(c>0)到相应准线l的距离为3,过焦点F的直线与椭圆交于A、B两点。
的离心率为,且其焦点F(c,0)(c>0)到相应准线l的距离为3,过焦点F的直线与椭圆交于A、B两点。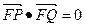

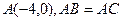 ,且
,且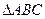 的内切圆方程为
的内切圆方程为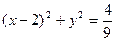 .
.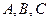 三点的椭圆标准方程;
三点的椭圆标准方程;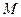 作圆的切线,求切线长最短时的点
作圆的切线,求切线长最短时的点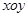 中,已知△
中,已知△ 顶点
顶点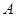 (-4,0)和
(-4,0)和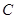 (4,0),顶点
(4,0),顶点 在椭圆
在椭圆 上,则
上,则 = ( )
= ( )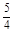
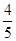
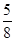
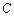 的方程为
的方程为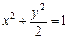 ,点
,点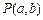 的坐标满足
的坐标满足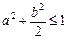
 过点
过点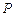 的直线
的直线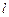 与椭圆交于
与椭圆交于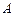 、
、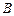 两点,点
两点,点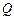 为线段
为线段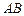 的中点,求:
的中点,求: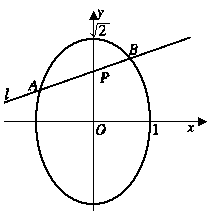
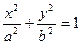 (a>b>0)的上顶点为A,左顶点为B, F为右焦点, 过F作平行与AB的直线交椭圆于C、D两点. 作平行四边形OCED, E恰在椭圆上.
(a>b>0)的上顶点为A,左顶点为B, F为右焦点, 过F作平行与AB的直线交椭圆于C、D两点. 作平行四边形OCED, E恰在椭圆上.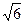 , 求椭圆方程.
, 求椭圆方程.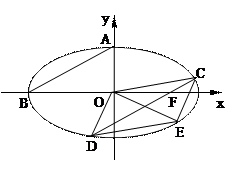
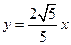 和
和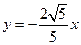 上的两个动点,并且
上的两个动点,并且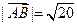 ,动点P满足
,动点P满足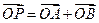 .记动点P的轨迹为C.
.记动点P的轨迹为C.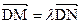 ,求实数
,求实数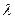 的取值范围.
的取值范围.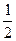 ,tan∠MNP=-2,适当建立坐标系,求以M、N为焦点,且过点P的椭圆方程.
,tan∠MNP=-2,适当建立坐标系,求以M、N为焦点,且过点P的椭圆方程.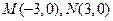 ,若直线上存在点P,使得
,若直线上存在点P,使得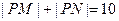 ,则称该直线为“A型直线”。给出下列直线:①
,则称该直线为“A型直线”。给出下列直线:① ;②
;②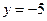 ;③
;③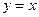 ;④
;④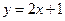 ,其中是“A型直线”的是
,其中是“A型直线”的是