题目内容
17.已知F1,F2分别是双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{9}=1(a>0)$的左右焦点,点P是双曲线上任一点,且||PF1|-|PF2||=2,顶点在原点且以双曲线的右顶点为焦点的抛物线为L.(Ⅰ)求双曲线C的渐近线方程和抛物线L的标准方程;
(Ⅱ)过抛物线L的准线与x轴的交点作直线,交抛物线于M、N两点,问直线的斜率等于多少时,以线段MN为直径的圆经过抛物线L的焦点?
分析 (Ⅰ)由双曲线的定义可知,2a=2,即a=1,即可得到双曲线C的渐近线方程,即可求出抛物线L的焦点坐标为A(1,0),即可求出抛物线L的标准方程;
(Ⅱ)设直线MN的斜率为k,则其方程为y=k(x+1).联立方程组,得到得k2x2+2(k2-2)x+k2=0,设M(x1,y1),N(x2,y2),根据韦达定理和MF⊥NF,即可求出k的值.
解答 解:(Ⅰ)由双曲线的定义可知,2a=2,即a=1.
∴双曲线的标准方程为${x^2}-\frac{y^2}{9}=1$.
∴双曲线的渐近线方程 y=±3x.
双曲线的右顶点坐标为A(1,0),即抛物线L的焦点坐标为A(1,0),
∴抛物线L的标准方程为y2=4x,
(Ⅱ)抛物线y2=4x的准线与对称轴的交点为(-1,0).
设直线MN的斜率为k,则其方程为y=k(x+1).
由$\left\{\begin{array}{l}y=k(x+1)\\{y^2}=4x\end{array}\right.$,得k2x2+2(k2-2)x+k2=0.
∵直线MN与抛物线交于M、N两点,
∴△=4(k2-2)2-4k4>0,解得-1<k<1.
设M(x1,y1),N(x2,y2),抛物线焦点为F(1,0),
∵以线段MN为直径的圆经过抛物线焦点,∴MF⊥NF.
∴$\frac{y_1}{{{x_1}-1}}•\frac{y_2}{{{x_2}-1}}=-1$,即y1y2+x1x2-(x1+x2)+1=0.
又${x_1}+{x_2}=-\frac{{2({k^2}-2)}}{k^2}$,x1x2=1,$y_1^2y_2^2=4{x_1}•4{x_2}=16$且y1,y2同号,
∴$\frac{{2({k^2}-2)}}{k^2}=-6$.解得${k^2}=\frac{1}{2}$,∴$k=±\frac{{\sqrt{2}}}{2}$.
即直线的斜率等于$±\frac{{\sqrt{2}}}{2}$时,以线段MN为直径的圆经过抛物线的焦点.
点评 本题是一道直线与圆锥曲线的综合题,韦达定理,考查分析问题、解决问题及计算能力,注意解题方法的积累,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 命题“?x>1,x2-1>0”的否定是“?x>1,x2-1≤0” | |
| B. | “x=2”是“x2-x-2=0”的充分不必要条件 | |
| C. | 若“p∧q”为假命题,则p,q均为假命题 | |
| D. | 命题“若a•b=0,则a=0或b=0”的否命题为“若a•b≠0,则a≠0且b≠0” |
| A. | {1,4,5} | B. | {2,3} | C. | {4,5} | D. | {1,5} |
| A. | a=-5或a=-15 | B. | a=-5或a=15 | C. | a=5或a=-15 | D. | a=5或a=15 |
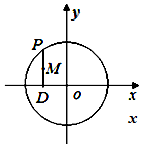 如图,在圆x2+y2=16上任取一点P,过点P作x 轴的垂线段PD,D为垂足,当点P在圆上运动时,则线段PD的中点M的轨迹方程为$\frac{x^2}{16}+\frac{y^2}{4}=1$.
如图,在圆x2+y2=16上任取一点P,过点P作x 轴的垂线段PD,D为垂足,当点P在圆上运动时,则线段PD的中点M的轨迹方程为$\frac{x^2}{16}+\frac{y^2}{4}=1$. | A. | 2 | B. | 3 | C. | 4 | D. | 5 |
| A. | x2=8y | B. | x2=-8y | C. | y2=-8x | D. | y2=8x |