题目内容
10.为研究质量x(单位:g)对弹簧长度y(单位:cm)的影响,对不同质量的6个物体进行测量,数据如下表所示:| x/g | 5 | 10 | 15 | 20 | 25 | 30 |
| y/g | 7.25 | 8.12 | 8.95 | 9.90 | 10.9 | 11.8 |
(2)求出R2;
(3)进行残差分析.
分析 (1)代入回归系数公式计算回归系数,得出回归方程;
(2)根据公式计算R2;
(3)根据计算的R2的大小进行分析.
解答 解:(1)作出散点图如下:
$\overline{x}$=$\frac{1}{6}$×(5+10+15+20+25+30)=17.5,
$\overline{y}$=$\frac{1}{6}$×(7.25+8.12+8.95+9.90+10.9+11.8)=9.49.
$\sum_{i=1}^{6}({x}_{i}-\overline{x})({y}_{i}-\overline{y})$=(-12.5)×(-2.24)+(-7.5)×(-1.37)+(-2.5)×(-0.54)+2.5×0.41+7.5×1.41+12.5×2.31=80.1.
$\sum_{i=1}^{6}({x}_{i}-\overline{x})^{2}$=(-12.5)2+(-7.5)2+(-2.5)2+2.52+7.52+12.52=437.5.
∴$\stackrel{∧}{b}$=$\frac{80.1}{437.5}$≈0.18,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$=6.34.
∴y关于x的线性回归方程是$\stackrel{∧}{y}$=0.18x+6.34.
(2)$\stackrel{∧}{y}$1=7.24,$\stackrel{∧}{y}$2=8.14,$\stackrel{∧}{y}$3=9.04,$\stackrel{∧}{y}$4=9.94,$\stackrel{∧}{y}$5=10.84,$\stackrel{∧}{y}$6=11.74.
$\sum_{i=1}^{6}({y}_{i}-\stackrel{∧}{y})^{2}$=0.012+0.022+0.092+0.042+0.062+0.062=0.0174.
$\sum_{i=1}^{6}({y}_{i}-\overline{y})^{2}$=2.242+1.372+0.542+0.412+1.412+2.312=12.9384.
∴R2=1-$\frac{0.0174}{12.9386}$=0.999.
(3)∵R2=0.999,非常接近1,故用回归方程$\stackrel{∧}{y}$=0.18x+6.34模拟x,y间的关系的拟合效果非常好.
点评 本题考查了线性回归方程的解法,回归方程拟合效果分析,计算较复杂,属于中档题.

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案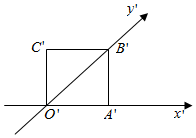 如图,正方形O′A′C′B′的边长为1cm,它是水平放置的一个平面图形的直观图,则它的原图形面积和直观图面积之比是( )
如图,正方形O′A′C′B′的边长为1cm,它是水平放置的一个平面图形的直观图,则它的原图形面积和直观图面积之比是( )| A. | 2$\sqrt{2}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | 2(1+$\sqrt{3}$) | D. | 6 |
| A. | f(x)=x2 | B. | f(x)=x | C. | f(x)=$\sqrt{x}$ | D. | f(x)=$\frac{1}{x}$ |
| A. | -e | B. | e | C. | 2e | D. | 3e |
| A. | 6$\sqrt{5}$ | B. | 12 | C. | 6$\sqrt{3}$ | D. | 6$\sqrt{2}$ |
 已知函数f(x)=2sin(ωx+$\frac{π}{4}$)在一个周期内的图象如图所示.
已知函数f(x)=2sin(ωx+$\frac{π}{4}$)在一个周期内的图象如图所示.