题目内容
如图, 、
、 是两个小区所在地,
是两个小区所在地, 、
、 到一条公路
到一条公路 的垂直距离分别为
的垂直距离分别为
 ,
,
 ,
, 两端之间的距离为
两端之间的距离为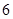
 .
.
(1)某移动公司将在 之间找一点
之间找一点 ,在
,在 处建造一个信号塔,使得
处建造一个信号塔,使得 对
对 、
、 的张角与
的张角与 对
对 、
、 的张角相等,试确定点
的张角相等,试确定点 的位置.
的位置.
(2)环保部门将在 之间找一点
之间找一点 ,在
,在 处建造一个垃圾处理厂,使得
处建造一个垃圾处理厂,使得 对
对 、
、 所张角最大,试确定点
所张角最大,试确定点 的位置.
的位置.
(1)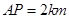 ;(2)
;(2)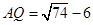
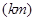 .
.
解析试题分析:(1)设?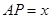 ,我们只要利用已知
,我们只要利用已知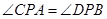 列出关于
列出关于 的方程即可,而这个方程就是在两个三角形中利用正切的定义,
的方程即可,而这个方程就是在两个三角形中利用正切的定义, ,
,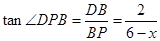 ,因此有
,因此有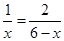 ,解之得;实际上本题可用相似形知识求解,
,解之得;实际上本题可用相似形知识求解,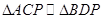 ,则
,则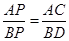 ,由引开出方程解出
,由引开出方程解出 ;(2)要使得
;(2)要使得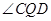 最大,可通过求
最大,可通过求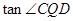 ,因为
,因为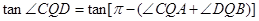
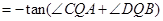 ,只要设
,只要设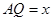 ,则
,则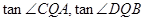 都可用
都可用 表示出来,从而把问题转化为求函数的最值,同(1)可得
表示出来,从而把问题转化为求函数的最值,同(1)可得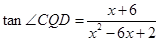 ,这里我们用换元法求最值,令
,这里我们用换元法求最值,令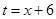 ,则有
,则有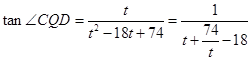 ,注意到
,注意到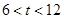 ,
,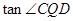 可取负数,即
可取负数,即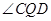 为钝角,因此在
为钝角,因此在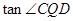 取负值中的最小值时,
取负值中的最小值时,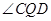 取最大值.
取最大值.
(1)设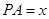 ,
,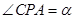 ,
,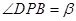 .
.
依题意有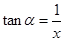 ,
, . 3分
. 3分
由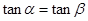 ,得
,得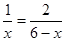 ,解得
,解得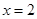 ,故点
,故点 应选在距
应选在距 点2
点2 处. 6分
处. 6分
(2)设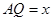 ,
,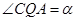 ,
,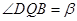 .
.
依题意有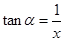 ,
, ,
,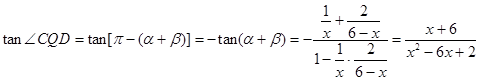 10分
10分
令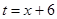 ,由
,由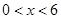 ,得
,得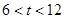 ,
,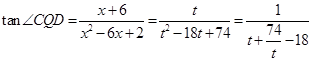 ,
,
12分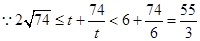 ,
,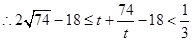 ,
,
当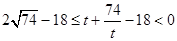 ,所张的角为钝角,最大角当
,所张的角为钝角,最大角当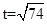 ,即
,即 时取得,故点
时取得,故点 应选在距
应选在距 点
点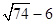
 处. 14分
处. 14分
考点:(1)角相等的应用与列方程解应用题;(2)角与函数的最大值.

练习册系列答案
相关题目
 ≥0对一切实数
≥0对一切实数 恒成立.
恒成立. ,若
,若 .
. ,求
,求 的单调递增区间.
的单调递增区间. 是三内角对应的三边,已知
是三内角对应的三边,已知 .(1)求角A的大小;(2)若
.(1)求角A的大小;(2)若 =
=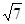 ,且△ABC的面积为
,且△ABC的面积为 ,求
,求 的值.
的值. .
. 的值.
的值. 中,已知
中,已知 ,
, 且
且 .
. 和
和 的值;
的值; ,求边
,求边 的长.
的长. ,
,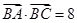 .
.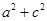 的值;
的值; 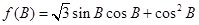 的值域.
的值域.
