题目内容
已知集合A=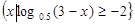 与B=
与B= 满足A∩B=
满足A∩B= ,求实数k的取值范围。
,求实数k的取值范围。
k≤-1或k=0或k≥3.
解析试题分析:易得A={x|-1≤x<3},对B通分可得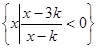 ,有两个实根k,3k,对两根大小分类,分k>0,k=0,k<0加以讨论,当k>0时,B=(k,3k), 欲满足A∩B=
,有两个实根k,3k,对两根大小分类,分k>0,k=0,k<0加以讨论,当k>0时,B=(k,3k), 欲满足A∩B= ,有k≥3;k=0,显然式子是不成立的,则B=
,有k≥3;k=0,显然式子是不成立的,则B= ,显然满足A∩B=
,显然满足A∩B= ;k<0可参考k>0,情形类似,综上,即可得答案.
;k<0可参考k>0,情形类似,综上,即可得答案.
试题解析:集合A等价于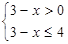 ,得A={x|-1≤x<3},
,得A={x|-1≤x<3},
B= =
=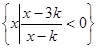 ,当k>0时,B=(k,3k), 欲满足A∩B=
,当k>0时,B=(k,3k), 欲满足A∩B= ,有k≥3;
,有k≥3;
当k=0时,B= ,显然满足A∩B=
,显然满足A∩B= ;当k<0时,B=(3k,k), 欲满足A∩B=
;当k<0时,B=(3k,k), 欲满足A∩B= ,有k≤-1.
,有k≤-1.
综上,k≤-1或k=0或k≥3.
考点:对数不等式,分式不等式,分类讨论.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
 ,若
,若 ,则实数
,则实数 = .
= . .
. ;
; ,若
,若 恰有3个元素,求
恰有3个元素,求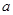 的取值范围.
的取值范围. ,
,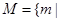 关于
关于 的方程
的方程 有实数根},
有实数根},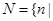 关于
关于 有实数根},
有实数根}, .
. ,
, .
. ,求实数
,求实数 的取值范围;
的取值范围; ,求实数
,求实数 ,求实数
,求实数 }.
}. ,
, ,则
,则 (
(
 )
) ______.
______. ,
, ,则
,则 _____________.
_____________.