题目内容
设全集 ,
,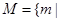 关于
关于 的方程
的方程 有实数根},
有实数根},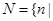 关于
关于 的方程
的方程 有实数根},
有实数根}, .
.
 .
.
解析试题分析:集合M中表示的方程有实数根,需要对方程的二次项系数是否为零分类讨论,若是一元一次方程,显然有实数根,若是一元二次,则需满足 ,从而可得
,从而可得 ,而集合N中表示的方程一定是一元二次方程,若有实数根,则需满足
,而集合N中表示的方程一定是一元二次方程,若有实数根,则需满足 ,从而可得
,从而可得 ,因此
,因此 .
.
试题解析:当 时,
时, ,即
,即 ;当
;当 时,
时, 即
即 ,且
,且 ,
,
∴ ,∴
,∴ ,
,
而对于 ,
, 即
即 ,∴
,∴ ,∴
,∴ .
.
考点:1.一元二次方程根的判别式;2.集合的运算.

练习册系列答案
相关题目
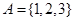 ,则它的真子集有8个;
,则它的真子集有8个;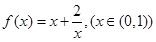 的值域为
的值域为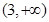 ;
; 的定义域为
的定义域为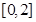 ,则函数
,则函数 的定义域为
的定义域为 ;
; 的定义在R上的奇函数,当
的定义在R上的奇函数,当 时,
时,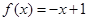 ,则当
,则当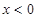 时,
时,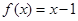
 (其中
(其中 为常数,
为常数,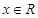 ),若
),若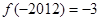 ,则
,则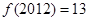 ;其中正确的是 (只写序号)。
;其中正确的是 (只写序号)。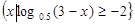 与B=
与B= 满足A∩B=
满足A∩B= ,求实数k的取值范围。
,求实数k的取值范围。 ,其中
,其中 },B="{x|"
},B="{x|"  },且A
},且A  B = R,求实数
B = R,求实数 的取值范围.
的取值范围.
 集合C=
集合C= 并且
并且 ,求a的取值范围.
,求a的取值范围. ,函数
,函数 的定义域为集合
的定义域为集合 ,集合
,集合 .
.
 ;
; ,
, ,求实数
,求实数 的取值范围.
的取值范围. ,
, ,
, ,则
,则 ________
________